Next: 演習問題 Up: 3つの境界値問題(three boundary value problems) Previous: 演習問題 目次 索引
 ,時刻
,時刻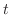 において弦の垂直方向の変位
において弦の垂直方向の変位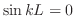 がみたす偏微分方程式について考えてみましょう.
がみたす偏微分方程式について考えてみましょう.
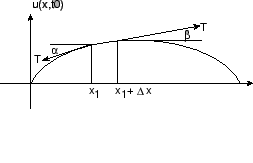
まず2点間に張った弦を考えます.弦をはじいて振動させます.このとき振幅は小さいものとします.また弦の張力は他の力に比べて大きいものとします.振動している弦の方程式をみつけるため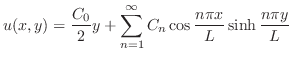 から
から
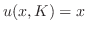 の間の弦の小さな部分について調べます.
の間の弦の小さな部分について調べます.
水平方向には動きがないので,水平方向の力はつりあっています.よって
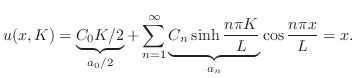 定数
定数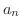 水平方向
水平方向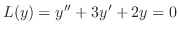
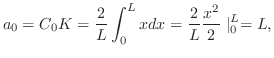 と加速度
と加速度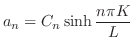 の積で表わされます.ただし
の積で表わされます.ただし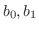 は単位長での質量,
は単位長での質量,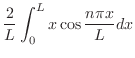 はいま考えている弦の小さな部分の長さ.よって
はいま考えている弦の小さな部分の長さ.よって
 垂直方向
垂直方向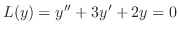
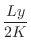 . 両辺を
. 両辺を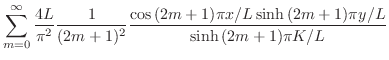 で割ると
で割ると
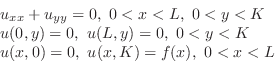
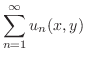 で割り,接線の傾きと微分係数は等しいことを用いると,
で割り,接線の傾きと微分係数は等しいことを用いると,
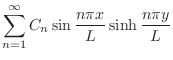
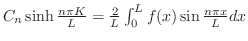 とすると,
とすると,
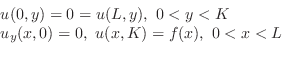 または
または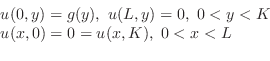
初期条件は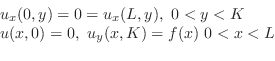 のときの弦の形状および初速度を指定する条件です.たとえば,初期の形状が
のときの弦の形状および初速度を指定する条件です.たとえば,初期の形状が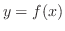 である弦に初速度
である弦に初速度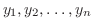 を与えた場合には,初期条件は
を与えた場合には,初期条件は
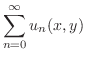
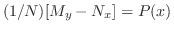 をもつとき,境界条件については,たとえば次のものが考えられます.
をもつとき,境界条件については,たとえば次のものが考えられます.
(i) 弦の両端を固定するとき
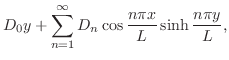
(ii) 弦の両端点が振動方向に自由に動けるとき
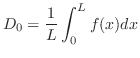
薄い膜の振動は,膜が静止の状態では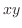 平面に位置し,時刻
平面に位置し,時刻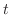 における垂直方向の変位が
における垂直方向の変位が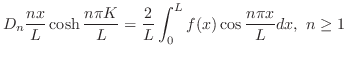 であるとすると,次の二次元波動方程式(two dimensional wave equation)で表わされます.
であるとすると,次の二次元波動方程式(two dimensional wave equation)で表わされます.
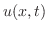
 で表わすと,次のようになります.
で表わすと,次のようになります.
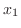
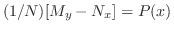 の水平に張られた弾性弦の初期形状が
の水平に張られた弾性弦の初期形状が で与えられているとき,この弦の垂直方向の変位を求めよ.
で与えられているとき,この弦の垂直方向の変位を求めよ.
解
まず弾性弦の垂直方向の変位を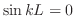 とすると,
とすると,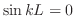 は一次元波動方程式
は一次元波動方程式
 を満たす.次に,初期条件は
を満たす.次に,初期条件は
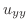
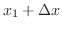
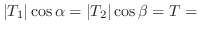 とおき,一次元波動方程式に代入すると
とおき,一次元波動方程式に代入すると
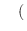
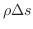
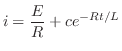 の境界条件を用いると,すべての
の境界条件を用いると,すべての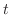 に対して
に対して
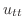
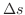
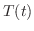 が0でないならば,
が0でないならば,
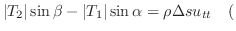 を意味する.よってこれよりSturn-Liouville問題
を意味する.よってこれよりSturn-Liouville問題
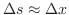
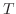 ,固有関数
,固有関数
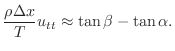 をもっている.さらに,固有値が
をもっている.さらに,固有値が
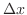 のとき,
のとき,
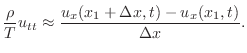
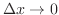
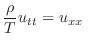 と
と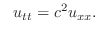 の積
の積
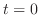
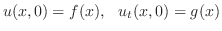
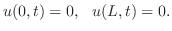 より,
より,
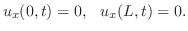
 に収束するように
に収束するように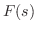 を選ばなければならない.ところがこれは皆さんがよく知っている関数
を選ばなければならない.ところがこれは皆さんがよく知っている関数 の
の![$[0,L]$](img1818.png) でのフーリエ正弦級数展開である.よって
でのフーリエ正弦級数展開である.よって
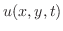
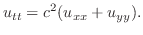 を見つける方法もほとんど同じである.
を見つける方法もほとんど同じである.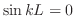 が
が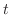 について項別微分可能であるとすると,
について項別微分可能であるとすると,
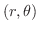
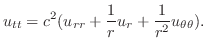 は0のフーリエ正弦級数となるので
は0のフーリエ正弦級数となるので
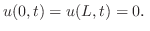

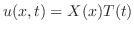 |
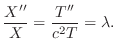 |
||
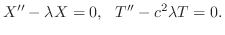 |
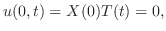 |
||
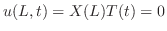 |
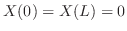 |
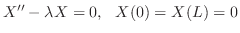 のとき解け.
のとき解け.
解
変数分離法を用い,
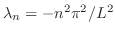 を仮定し,これを二次元波動方程式に代入すると
を仮定し,これを二次元波動方程式に代入すると
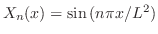
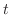 と独立であり,右辺は
と独立であり,右辺は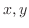 と独立なので,両辺とも定数となり,この定数を
と独立なので,両辺とも定数となり,この定数を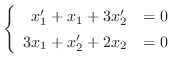 とおくと
とおくと
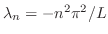
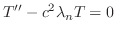
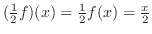 とおくと次の3つの微分方程式を得る.
とおくと次の3つの微分方程式を得る.
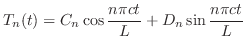
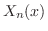
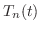
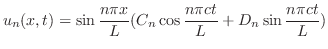 . ここで境界条件
. ここで境界条件
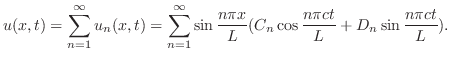
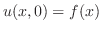
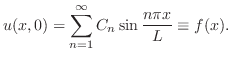
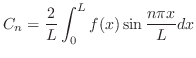 |
 |
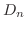 |
|
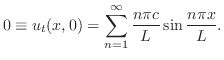 |
 |
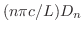 |
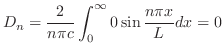 に対して,
に対して,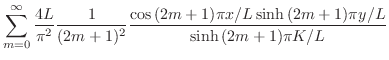 は
は
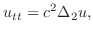
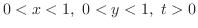 より
より
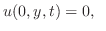 となるので
となるので
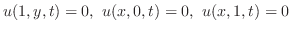 .よって
.よって
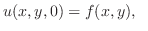
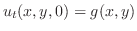
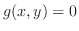
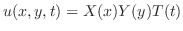 が満たされるためには
が満たされるためには
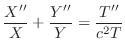
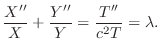 を定めよう.
を定めよう.
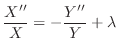
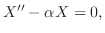
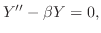 |
 |
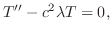 |
|
 |
![$\displaystyle \frac{2}{1}\int_{0}^{1}[\frac{2}{1}\int_{0}^{1}f(x,y)\sin{m\pi x}dx]\sin{n\pi y}dy$](img2215.png) |
||
 |
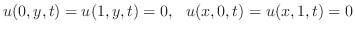 |
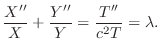 を
を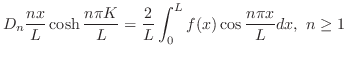 に代入すると解が得られる.
に代入すると解が得られる.
