Next: 演習問題 Up: 3つの境界値問題(three boundary value problems) Previous: 3つの境界値問題(three boundary value problems) 目次 索引

 級の関数で,Laplace方程式をみたすものを調和関数(harmonic function)といいます.
級の関数で,Laplace方程式をみたすものを調和関数(harmonic function)といいます.
二次元のLaplace方程式の解は次の形のいずれかを取ることを学びましたが,次の形の関数の有限個の一次結合でLaplace方程式の境界値問題の解を表わすのが適当でないことがよくあります.






解
変数分離法と境界条件
 よりLaplace方程式の解は
よりLaplace方程式の解は

 をすべての
をすべての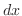 でみたし,また2番目の形も
でみたし,また2番目の形も
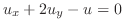 のとき,つまり
のとき,つまり
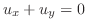 のとき境界条件
のとき境界条件
 をすべての
をすべての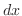 でみたす.よって重ね合わせの原理より,
でみたす.よって重ね合わせの原理より,
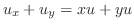
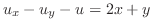 より
より
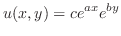
 に収束するように
に収束するように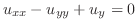 を選ばなければならない.ところが,これは本質的にフーリエ余弦級数である.よって
を選ばなければならない.ところが,これは本質的にフーリエ余弦級数である.よって
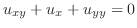
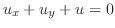 |
 |
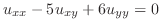 |
|
 |
![$\displaystyle \frac{2L}{n^{2}\pi^{2}}[(-1)^{n} - 1] = \left\{\begin{array}{cl}
...
...}{n^{2}\pi^{2}}, & n \mbox{odd} \\
0, & n \mbox{even}.
\end{array}\right .$](img2114.png) |
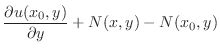 |
 |
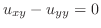 |
|
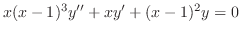 |
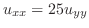 |
