Next: 演習問題 Up: 偏微分方程式 Previous: 偏微分方程式 目次 索引
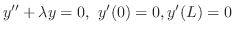 ,これらの変数の関数
,これらの変数の関数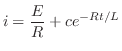 ,偏導関数
,偏導関数
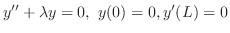 を含んだ方程式のことです.この方程式の次数は偏導関数の最高次数で与えられます.
を含んだ方程式のことです.この方程式の次数は偏導関数の最高次数で与えられます.
最も一般的な2変数の2階線形偏微分方程式は次の形で与えられます.
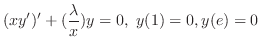
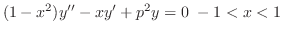 は
は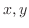 の既知の関数とします.また独立変数
の既知の関数とします.また独立変数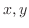 が定義されている平面上の領域で上の式を満たす
が定義されている平面上の領域で上の式を満たす をこの偏微分方程式の解といいます.
をこの偏微分方程式の解といいます.
線形偏微分方程式は比較的簡単な理論で説明でき,また多くの実用問題での数学的モデルはこの形で与えられるので,しっかり学んで下さい.
次の演算記号は偏微分方程式を扱う上で欠かせないものです.
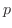 |
 |
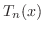 Laplace or potential operator Laplace or potential operator |
|
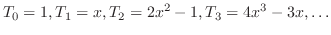 |
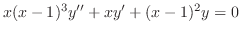 |
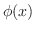 Heat または diffusion operator Heat または diffusion operator |
|
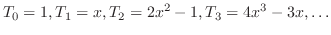 |
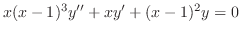 |
 D'Alembert or wave operator D'Alembert or wave operator |
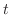 は時間変数,
は時間変数,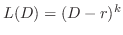 は物質の熱伝導率/熱拡散率に反比例する定数,
は物質の熱伝導率/熱拡散率に反比例する定数,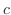 は波動の速度を表わします.
は波動の速度を表わします.
定数係数の場合,2次曲線

 が負,零,正にしたがって,楕円型(elliptic),放物線型(parabolic),双曲線型(hyperbolic)とよばれます.また適当な変数変換により
が負,零,正にしたがって,楕円型(elliptic),放物線型(parabolic),双曲線型(hyperbolic)とよばれます.また適当な変数変換により
 が負,零,正にしたがって,potential operator,diffusion operator,wave operatorを用いることができます.
が負,零,正にしたがって,potential operator,diffusion operator,wave operatorを用いることができます.
 は楕円型であることを示せ.また,
は楕円型であることを示せ.また,
 は何型か調べよ.
は何型か調べよ.解

一方,
 は
は

 のとき楕円型,
のとき楕円型, のとき放物線型,
のとき放物線型, のとき双曲線型となる.
のとき双曲線型となる.

解


 .
.

偏微分方程式の解全体の集合は解集合(solution set)といいます.ただ解集合は非常に大きな集合であったり,やっかいな集合であったりするので,私たちはすべての解が導けるような基本的な解の集合を考えます.このような解の集合を完全解(complete solution)または一般解(general solution)といいます.また特殊解は一般解から導けます.
簡単な偏微分方程式は次の例が示すように直接積分することにより解くことができます.
 を解け.
を解け.解

 は
は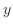 の任意の関数.
の任意の関数.

 を解け.
を解け.解

 |
 |
 |
|
 |
 |
残念ながら一般に,偏微分方程式は上で行なったように直接積分して解けることはほとんどありません.そこで次の節では他の方法を考えてみます.その前に,もう少し偏微分方程式の解について考えます.
同次常微分方程式で解の一次結合が,また解であったように,同次偏微分方程式でも
 が,同次偏微分方程式の解ならば,その一次結合
が,同次偏微分方程式の解ならば,その一次結合
 もまた解になります.とくに,偏微分方程式では
もまた解になります.とくに,偏微分方程式では
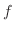 が収束し,この級数の項別微分が可能であれば,
が収束し,この級数の項別微分が可能であれば,
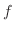 も同次偏微分方程式の解になります.これを重ね合わせの原理(principle of superposition)といいよく用います.
も同次偏微分方程式の解になります.これを重ね合わせの原理(principle of superposition)といいよく用います.