Next: 偏微分方程式 Up: Sturm-Liouville 問題(Srurm-Liouville problem) Previous: Sturm-Liouville 問題(Srurm-Liouville problem) 目次 索引
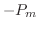
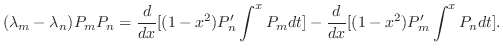
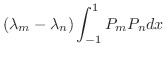
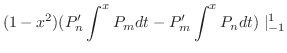
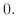 が負でない整数のとき,この方程式は多項式の解をもちます.この解を
が負でない整数のとき,この方程式は多項式の解をもちます.この解を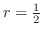 のとき
のとき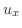 になるようにし
になるようにし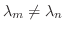 で表わします.これを位数
で表わします.これを位数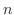 のChebyshevの多項式といいます.最初のいくつかのChebyshevの多項式を表わすと次のようになります.
のChebyshevの多項式といいます.最初のいくつかのChebyshevの多項式を表わすと次のようになります.
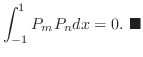
![$[-1,1]$](img1901.png) で直交系をなすことを示せ.
で直交系をなすことを示せ.