Next: 演習問題 Up: 1階微分方程式 Previous: 演習問題 目次 索引
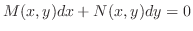
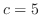 をかけて得られる方程式
をかけて得られる方程式
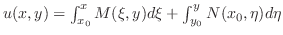
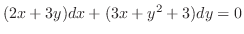 をこの微分方程式の積分因子(integrating factor)といいます.
をこの微分方程式の積分因子(integrating factor)といいます.
一般に,積分因子はひとつとは限りません.たとえば,関数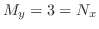 と
と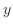 は次の微分方程式の積分因子です(本当か確認して).
は次の微分方程式の積分因子です(本当か確認して).
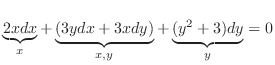
ではどうやって積分因子を見つけることができるか考えてみましょう.
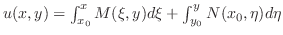
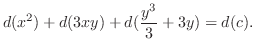
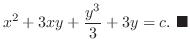
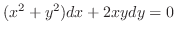 のとき
のとき
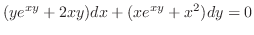
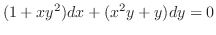
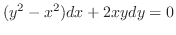
 だけの関数なら積分因子は
だけの関数なら積分因子は
![$\displaystyle \mu(x) = \exp\{\int\frac{1}{N}[M_{y} - N_{x}]dx\} $](img245.png)
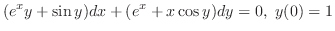 のとき
のとき
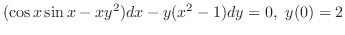
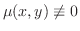
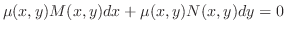
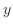 だけの関数なら積分因子は
だけの関数なら積分因子は
![$\displaystyle \mu(y) = \exp\{-\int\frac{1}{M}[M_{y} - N_{x}]dy\} $](img250.png)
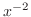 を解け.
を解け.
解
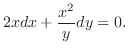 よりこの全微分方程式は完全微分形ではない.
そこで
よりこの全微分方程式は完全微分形ではない.
そこで
![$({1}/{N})[M_{y} - N_{x}]$](img253.png) を計算すると
を計算すると
![$\displaystyle \frac{1}{N}[M_{y} - N_{x}] = \frac{1}{x^{2}y - x}[1 - (2xy - 1)] = -\frac{2}{x} . $](img254.png)
 だけの関数なのでI.より積分因子は
だけの関数なのでI.より積分因子は
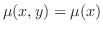
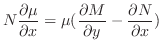
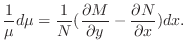
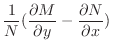

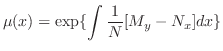 を解け.
を解け.
解
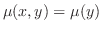 より完全微分形ではない.また
より完全微分形ではない.また
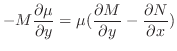 より
より
![$(1/N)[M_{y} - N_{x}], (1/M)[M_{y} - N_{x}]$](img262.png) ともに
ともに だけ
だけ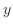 だけの関数ではない.そこで別な方法で積分因子を見つけてみる.
だけの関数ではない.そこで別な方法で積分因子を見つけてみる.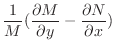 と
と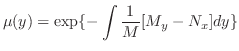 をよく見ると似た形をしている.そこで積分因子
をよく見ると似た形をしている.そこで積分因子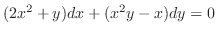 は
は
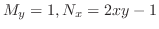 の形をしていると考えてみる.
の形をしていると考えてみる.
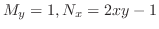 が積分因子なら
が積分因子なら
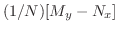
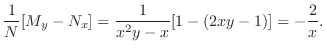 |
 |
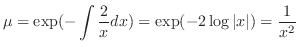 |
|
 |
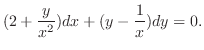 |
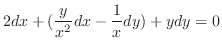
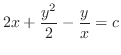 となるので,
となるので,