Next: 7.1 解答 Up: 演習問題解答 Previous: 6.3 解答 索引
6.4
1.
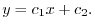
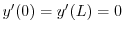 を用いると
を用いると
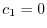 となり,
となり,
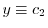 .
.
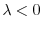 のとき,
のとき,
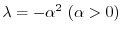 とおくと
とおくと
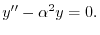
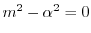 より,
より,
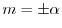 .よって
.よって
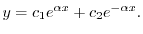
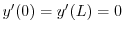 を用いると
を用いると
| 0 |  |
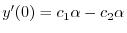 |
|
| 0 |  |
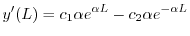 |
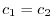 .また2つめの式より
.また2つめの式より
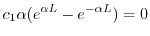
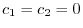 .よって
.よって
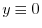 .
.
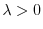 のとき,
のとき,
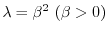 とおくと
とおくと
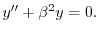
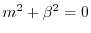 より,
より,
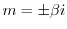 .よって
.よって
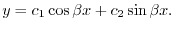
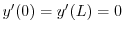 を用いると
を用いると
| 0 |  |
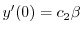 |
|
| 0 |  |
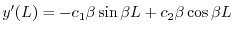 |
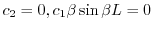 を得る.ここで
を得る.ここで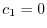 ならば自明でない解が存在しない.そこで自明でない解が存在するためには,
ならば自明でない解が存在しない.そこで自明でない解が存在するためには,
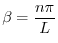 .よって
.よって
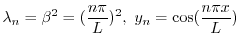
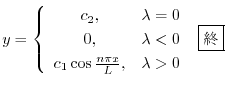
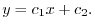
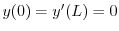 を用いると
を用いると
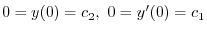
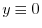 .
.
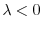 のとき,
のとき,
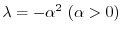 とおくと
とおくと
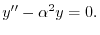
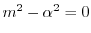 より,
より,
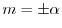 .よって
.よって
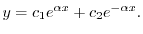
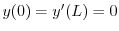 を用いると
を用いると
| 0 |  |
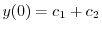 |
|
| 0 |  |
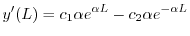 |
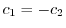 .また2つめの式より
.また2つめの式より
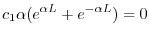
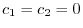 .よって
.よって
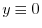 .
.
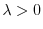 のとき,
のとき,
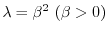 とおくと
とおくと
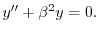
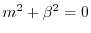 より,
より,
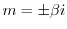 .よって
.よって
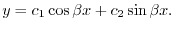
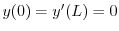 を用いると
を用いると
| 0 |  |
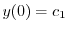 |
|
| 0 |  |
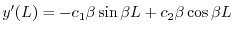 |
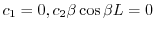 を得る.ここで
を得る.ここで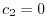 ならば自明でない解が存在しない.そこで自明でない解が存在するためには,
ならば自明でない解が存在しない.そこで自明でない解が存在するためには,
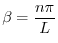 .よって
.よって
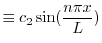 となる.これより
となる.これより
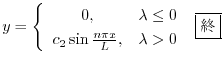
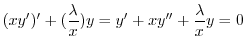
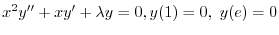
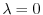 のとき,
のとき,
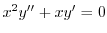 .これはCauchy-Eulerの方程式より
.これはCauchy-Eulerの方程式より
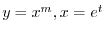 とおくと,
とおくと,
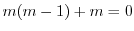 より
より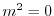 .よって
.よって
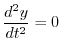
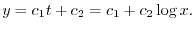
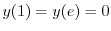 を用いると
を用いると
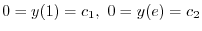
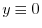 .
.
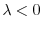 のとき,
のとき,
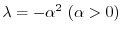 とおくと
とおくと
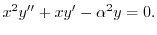
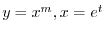 とおくと,
とおくと,
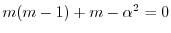 より
より
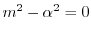 .よって
.よって
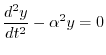
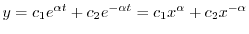
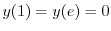 を用いると
を用いると
| 0 |  |
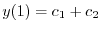 |
|
| 0 |  |
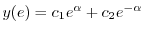 |
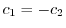 .また2つめの式より
.また2つめの式より
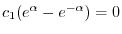
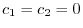 .よって
.よって
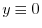 .
.
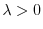 のとき,
のとき,
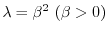 とおくと
とおくと
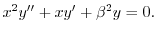
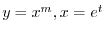 とおくと,
とおくと,
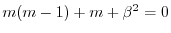 より
より
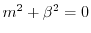 .よって
.よって
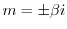 .
これより
.
これより
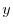 |
 |
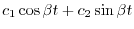 |
|
 |
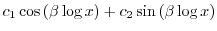 |
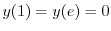 を用いると
を用いると
| 0 |  |
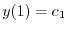 |
|
| 0 |  |
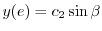 |
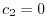 ならば自明でない解が存在しない.そこで自明でない解が存在するためには,
ならば自明でない解が存在しない.そこで自明でない解が存在するためには,
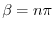 .よって
.よって
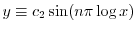 となる.
まとめると
となる.
まとめると
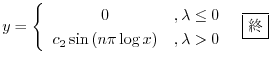
2. Chebyshevの多項敷き
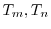 は固有値
は固有値
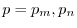 に関する固有関数である.よって
に関する固有関数である.よって
ここで式(A.14)に 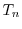 を式(A.15)に
を式(A.15)に 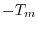 をかけて加えると
をかけて加えると
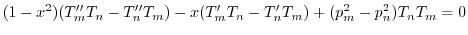
これは一階の線形微分方程式なので,積分因子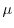 を求めると
を求めると
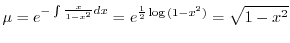
これを式(A.16)の両辺にかけると
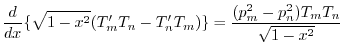
これを-1から1まで積分すると
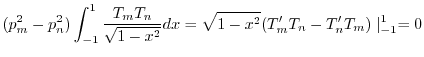
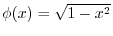 に関して,
に関して,
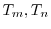 は直交する.
は直交する.
