Next: 5.1 ローラン展開 Up: 演習問題詳解 Previous: 4.3 コーシーの積分定理 索引
2. コーシーの積分表示
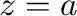 が曲線
が曲線 の内部にあり
の内部にあり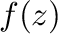 が曲線
が曲線 を含む領域で正則ならば
を含む領域で正則ならば
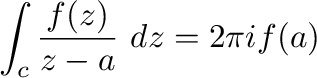
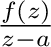 が曲線
が曲線 の内部で正則ならば
の内部で正則ならば
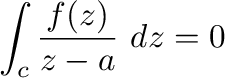
(a)
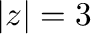 より
より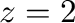 はこの曲線の内部にある.よって,コーシーの積分表示より
はこの曲線の内部にある.よって,コーシーの積分表示より
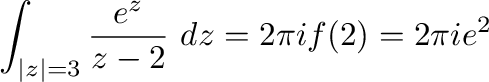
(b) 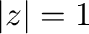 より
より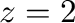 はこの曲線の内部にない.よって,被積分関数は正則となるのでコーシーの積分定理より
はこの曲線の内部にない.よって,被積分関数は正則となるのでコーシーの積分定理より
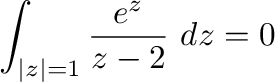
(c) 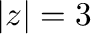 より
より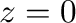 はこの曲線の内部にある.よって,コーシーの積分表示より
はこの曲線の内部にある.よって,コーシーの積分表示より
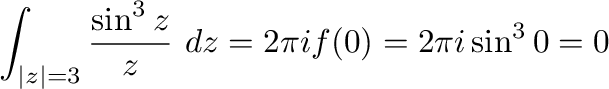
(d) 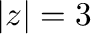 より
より
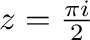 はこの曲線の内部にある.よって,コーシーの積分表示より
はこの曲線の内部にある.よって,コーシーの積分表示より
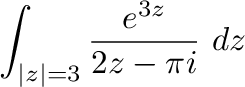 |
 |
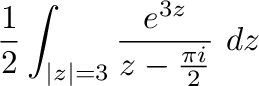 |
|
 |
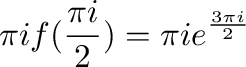 |
||
 |
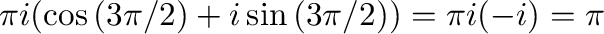 |
(e) 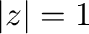 より
より
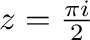 はこの曲線の内部にない.よって,被積分関数は正則となるのでコーシーの積分定理より
はこの曲線の内部にない.よって,被積分関数は正則となるのでコーシーの積分定理より
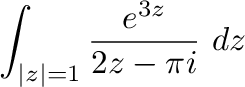 |
 |
0 |
(f) 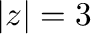 より
より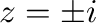 はこの曲線の内部にある.よって,コーシーの積分表示より
はこの曲線の内部にある.よって,コーシーの積分表示より
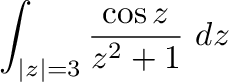 |
 |
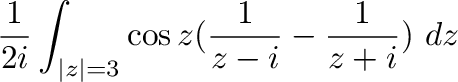 |
|
 |
![$\displaystyle \frac{1}{2i}[2\pi i (f(i) - f(-i))] = \pi[\cos{(i)} - \cos{(-i)}]$](img960.png) |
||
 |
![$\displaystyle \pi[\frac{e^{i^2} + e^{-i^2}}{2} - (\frac{e^{-i^2} + e^{i^2}}{2})] = 0$](img961.png) |
(g) 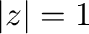 より
より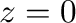 はこの曲線の内部にある.よって,コーシーの積分表示より
はこの曲線の内部にある.よって,コーシーの積分表示より
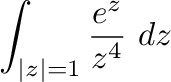 |
 |
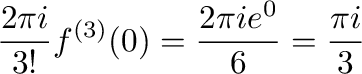 |
(h) 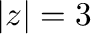 より
より
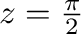 はこの曲線の内部にある.よって,コーシーの積分表示より
はこの曲線の内部にある.よって,コーシーの積分表示より
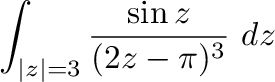 |
 |
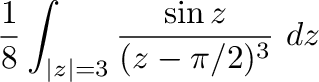 |
|
 |
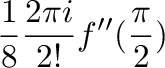 |
ここで
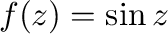 より
より
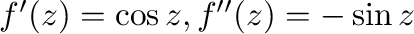 より
より
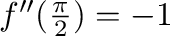 よって
よって
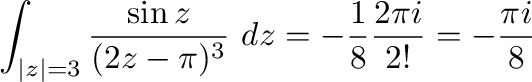
(i) 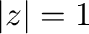 より
より
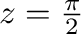 はこの曲線の内部にない.よって,被積分関数は正則となるのでコーシーの積分定理より
はこの曲線の内部にない.よって,被積分関数は正則となるのでコーシーの積分定理より
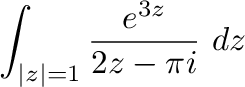 |
 |
0 |