Next: 初等関数の逆関数 Up: 初等関数 Previous: 有理関数 索引
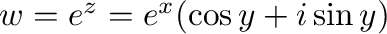 を指数関数といい,
を指数関数といい,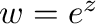 あるいは
あるいは
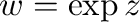 と表わす.
と表わす.
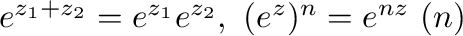
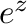 は周期
は周期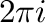 を持つ.
を持つ.
証明 (1)
 とすると,
とすると,
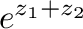 |
 |
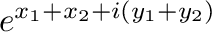 |
|
 |
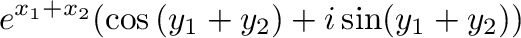 |
||
 |
![$\displaystyle e^{x_{1} + x_{2}}[\cos{y_{1}}\cos{y_{2}} - \sin{y_{1}}\sin{y_{2}} + i(\sin{y_{1}}\cos{y_{2}} + \cos{y_{1}}\sin{y_{2}})]$](img121.png) |
||
 |
![$\displaystyle e^{x_{1} + x_{2}}[(\cos{y_{1}} + i\sin{y_{1}})(\cos{y_{2}}+i\sin{y_{2}})]$](img122.png) |
||
 |
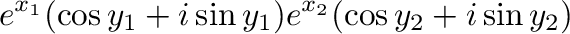 |
||
 |
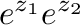 |
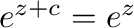 が成り立つとき,関数
が成り立つとき,関数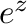 は周期
は周期 を持つという.
そこで,
を持つという.
そこで,
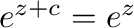 とおくと
とおくと
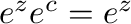 より
より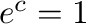 .
.
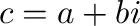 とおくと
とおくと
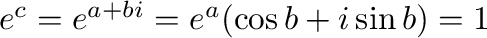 より
より
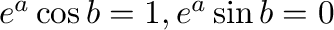 .これより
.これより
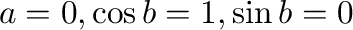 .これを満たす
.これを満たす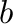 は
は
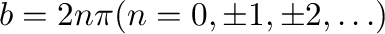 .したがって,
.したがって,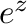 は周期
は周期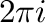 を持つ.
を持つ.
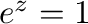
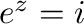
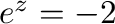
2. 次の値を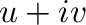 の形で表せ.
の形で表せ.
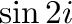
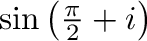
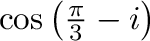
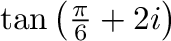
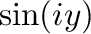
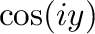
3. 次の公式を証明せよ.
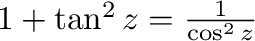
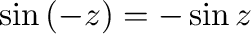
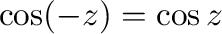
4. 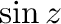 について次のことが成り立つことを示せ.
について次のことが成り立つことを示せ.
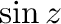 は周期
は周期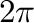 を持つ
を持つ
(5) 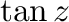 の周期を求めよ.
の周期を求めよ.