Next: 複素積分(complex integral) Up: 複素積分 Previous: 複素積分 索引
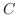 と
と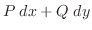 が
が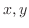 の実関数で曲線
の実関数で曲線 上の全ての点で連続であるとする.このとき,曲線
上の全ての点で連続であるとする.このとき,曲線 に沿った
に沿った
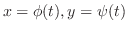 の 線積分(line integral)は
の 線積分(line integral)は
![$\displaystyle \int_{C} [P(x,y)\;dx + Q(x,y)\;dy]$](img365.png)
 が滑らかで,媒介変数表示
が滑らかで,媒介変数表示
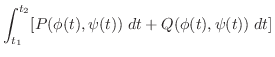 ,
,
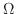 が可能なとき,線積分は
が可能なとき,線積分は
![$\displaystyle \int_{t_{1}}^{t_{2}}[P(\phi(t),\psi(t))\;dt + Q(\phi(t),\psi(t))\;dt]$](img368.png)
 を単一閉曲線とし,
を単一閉曲線とし,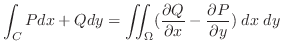 をその周および内部からなる閉領域とする.関数
をその周および内部からなる閉領域とする.関数
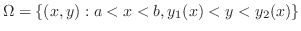 が
が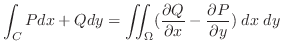 で連続な偏導関数をもつとき,
で連続な偏導関数をもつとき,
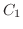
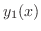
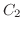
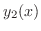
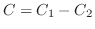
2. 媒介変数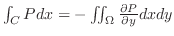 に関する次の線積分を求めよ.
に関する次の線積分を求めよ.
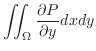
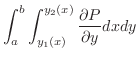
3. Greenの定理を用いて次の線積分の値を求めよ.
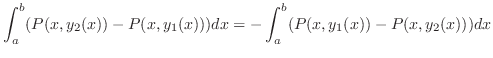 単位円周
単位円周
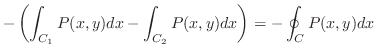 第1象限にある四分円の周
第1象限にある四分円の周