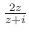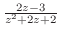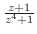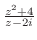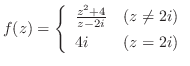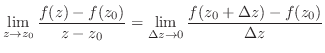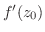Next: 正則関数(analytic function,holomorphic function) Up: 正則関数 Previous: 正則関数 索引
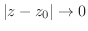 の近傍
の近傍
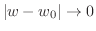 で定義された
で定義された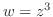 において,
において,
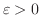 に対して
に対して
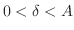 となるとき,つまり任意の正の数
となるとき,つまり任意の正の数
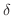 に対して,
に対して,
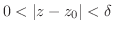 なる適当な
なる適当な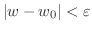 が定まり,
が定まり,
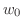 なるすべての
なるすべての に対して
に対して
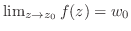 が成り立つとき,
が成り立つとき, は極限値
は極限値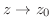 をもつといい,
をもつといい,
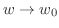 と書く.
と書く.
注
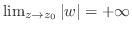 の方向は無数にあるが,どんな方向から
の方向は無数にあるが,どんな方向から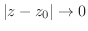 に近づいても,
に近づいても,
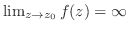 となることである.
となることである.
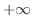 のとき
のとき
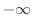 と定める.実関数の場合,
と定める.実関数の場合,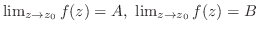 と
と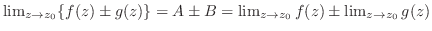 と2つの場合があったが,上の定義より複素関数の場合は
と2つの場合があったが,上の定義より複素関数の場合は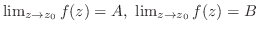 の場合しかない.
の場合しかない.
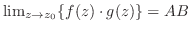 が存在して有限ならば
が存在して有限ならば
(1)
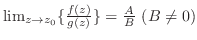
(2)
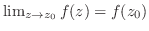
(3)
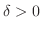
領域 で定義された
で定義された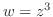 において,
において, 内の点
内の点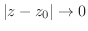 で
で
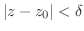 が成り立つとき,つまり任意の正の数
が成り立つとき,つまり任意の正の数
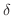 に対して適当な
に対して適当な
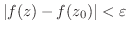 が定まって,
が定まって,
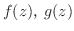 なる全ての
なる全ての に対して
に対して
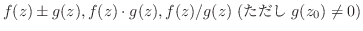 が成り立つとき,
が成り立つとき, は
は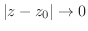 で連続であるという.
で連続であるという.
 が領域
が領域 の各点で連続のとき,
の各点で連続のとき, は
は で連続であるという.
で連続であるという.
(1) 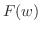 が
が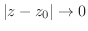 で連続であれば,
で連続であれば,
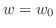 はいずれも
はいずれも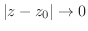 で連続である.
で連続である.
(2) 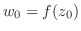 は
は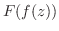 で連続,
で連続,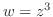 は
は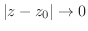 で連続で,
で連続で,
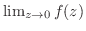 ならば合成関数
ならば合成関数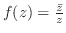 は
は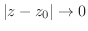 で連続である.
で連続である.
次の に対し,
に対し,
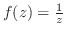 を調べよ.
を調べよ.
(1)
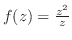
(2)
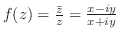
(3)
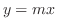
解
(1)
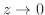 であるから,
であるから, が直線
が直線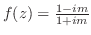 に沿って
に沿って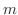 のとき
のとき
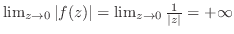 は
は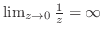 の価によって異なる価をとる.よって,
の価によって異なる価をとる.よって,
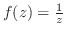 は存在しない.
は存在しない.
(2)
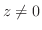 .よって
.よって
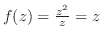
(3) 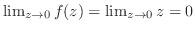 のとき,
のとき,
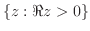 .よって
.よって
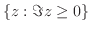 .
.
 平面から原点Oを除いた集合
平面から原点Oを除いた集合
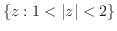
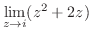
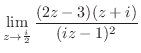
2. 次の極限値を求めよ.
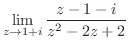
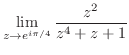
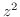
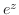
3. 次の関数が連続でない点を求めよ.