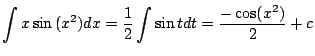Next: 部分積分法(integration by parts) Up: 積分法(INTEGRATION) Previous: 置換積分法(integration by substitution)
3.2
1.
(a) ![]() とおくと
とおくと
![]() より,与えられた積分はtの関数とdtで,すでに学んだ
より,与えられた積分はtの関数とdtで,すでに学んだ![]() の
の![]() についての積分として表せる.
についての積分として表せる.
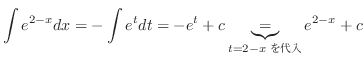
![]() とおくと
とおくと ![]() より,
より,
![]() の
の![]() についての積分として表せる.
についての積分として表せる.
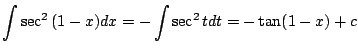
![]() とおくと
とおくと
![]() より
より
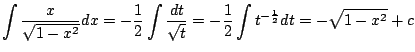
![]() とおくと
とおくと
![]() より
より
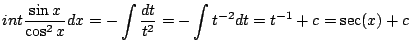
![]() とおくと
とおくと
![]() より
より
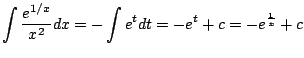
![]() とおくと
とおくと
![]() より
より
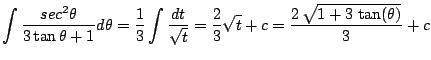
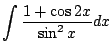 |
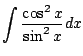 |
||
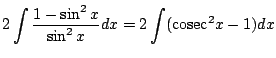 |
|||
![]() とおくと
とおくと
![]() より
より
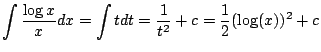
![]() とおくと
とおくと
![]() より
より
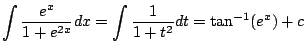
![]() とおくと
とおくと
![]() より
より