Next: 3.8 定積分の計算 Up: 確認問題詳解 Previous: 3.6 無理関数の積分法 索引
1.
1 区間![$[0,1]$](img146.png) を
を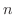 等分する.
等分する. 軸上の点
軸上の点
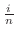 に対応する値
に対応する値
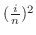 を高さとし,底辺が
を高さとし,底辺が
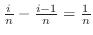 を底辺とする長方形を考える.この長方形を
を底辺とする長方形を考える.この長方形を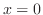 から
から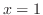 までの間で加えると,Riemann和とよばれる次の和を得る.
までの間で加えると,Riemann和とよばれる次の和を得る.
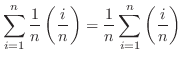
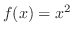 は区間
は区間![$[0,1]$](img146.png) で連続なので,
で連続なので,
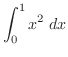 |
 |
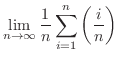 |
|
 |
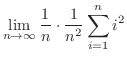 |
||
 |
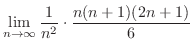 |
||
 |
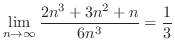 |
2.
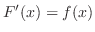 とすると
とすると
![$\displaystyle{\int_{a}^{b}f(x)\; dx = [F(x)]_{a}^{b} = F(a) - F(b)}$](img1919.png)
![$\displaystyle \int_{0}^{1}(x^2 + 3)\; dx = \left[\frac{x^3}{3} + 3x\right]_{0}^{1} = \frac{1}{3} + 3 = \frac{10}{3}$](img1920.png)
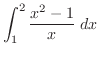 |
 |
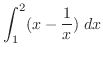 |
|
 |
![$\displaystyle \left[\frac{x^2}{2} - \log\vert x\vert\right]_{1}^{2}$](img1923.png) |
||
 |
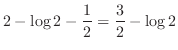 |
![$\displaystyle \int_{0}^{1}\sqrt{x^3}\; dx = \int_{0}^{1}x^{\frac{3}{2}}\; dx = \left[\frac{2}{5}x^{\frac{5}{2}}\right]_{0}^{1} = \frac{2}{5}$](img1925.png)
![$\displaystyle \int_{0}^{\pi}\cos{x}\; dx = [\sin{x}]_{0}^{\pi} = 0$](img1926.png)
![$\displaystyle \int_{0}^{\frac{\pi}{2}}\sin{x}\; dx = [-\cos{x}]_{0}^{\frac{\pi}{2}} = \cos{0} = 1$](img1927.png)
3.
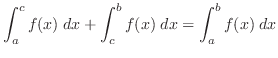
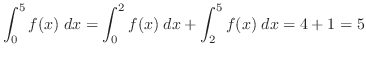
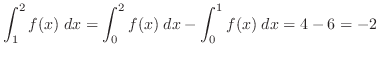
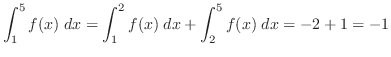
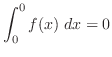
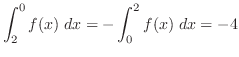
4.
微積分学の基本定理
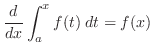
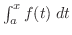 は
は の関数なので,これを
の関数なので,これを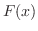 とおくと,左辺は
とおくと,左辺は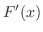 を求めることと同じである.
を求めることと同じである.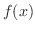 が物体の速さだとすると,
が物体の速さだとすると,
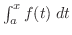 は速さ×時間より,時刻
は速さ×時間より,時刻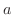 から
から までの間で動いた距離を表す.ということは,左辺は動いた距離の瞬間の変化を表している.しかし,動いた距離の瞬間の変化とは,速さのことである.したがって,右辺と等しい.
までの間で動いた距離を表す.ということは,左辺は動いた距離の瞬間の変化を表している.しかし,動いた距離の瞬間の変化とは,速さのことである.したがって,右辺と等しい.
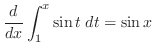
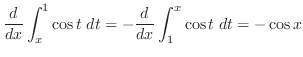
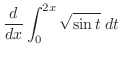 |
 |
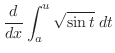 |
|
 |
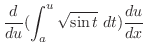 |
||
 |
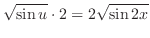 |
5.
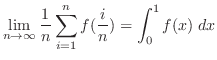
![$\displaystyle \lim_{n \to \infty}\frac{1}{n}\sum_{i=1}^{n}\frac{i}{n} = \int_{0}^{1}x\;dx = [\frac{x^2}{2}]_{0}^{1} = \frac{1}{2}$](img1946.png)
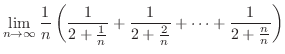 |
|||
 |
![$\displaystyle \int_{0}^{1}\frac{1}{2+x}\;dx = [\log\vert 2+x\vert]_{0}^{1}$](img1948.png) |
||
 |
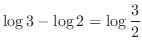 |
![$\displaystyle \lim_{n \to \infty}\frac{1}{n}\sqrt{\frac{i}{n}} =
\int_{0}^{1}\sqrt{x}\;dx = [\frac{2}{3}x^{3/2}]_{0}^{1} = \frac{2}{3}$](img1950.png) |