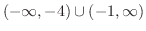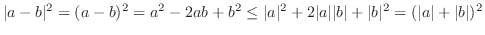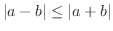Next: 1.1 関数 Up: 確認問題詳解 Previous: 0.1 数(NUMBERS) 索引
1.
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
![$(-\infty,1]$](img1035.png)
 |
 |
 |
|
 |
 |
 |
|
 |
 |
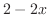 |
|
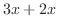 |
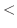 |
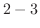 |
|
 |
 |
 |
|
 |
 |
 |
 |
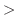 |
0 | |
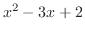 |
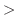 |
0 | |
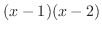 |
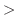 |
0 |
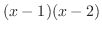 が0になるのは,1と2である.そこで,これらの点を数直線上に白抜きまるで印を付ける. これにより,数直線は次の3つの区間に分割される.
が0になるのは,1と2である.そこで,これらの点を数直線上に白抜きまるで印を付ける. これにより,数直線は次の3つの区間に分割される.
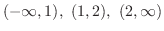
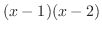 の符号(sgn)は変わらない.
の符号(sgn)は変わらない.
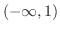 |
![${\rm sgn}[(x-1)(x-2)] = (-)(-) = +$](img1056.png) |
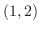 |
![${\rm sgn}[(x-1)(x-2)] = (+)(-) = -$](img1057.png) |
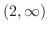 |
![${\rm sgn}[(x-1)(x-2)] = (+)(+) = +$](img1059.png) |
これより,不等式の解は
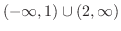 となる.
となる.
 |
 |
 |
|
 |
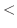 |
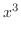 |
|
| 0 | 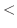 |
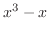 |
|
| 0 |  |
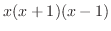 |
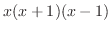 が0になるのは,-1,0と1である.そこで,これらの点を数直線上に白抜きまるで印を付ける. これにより,数直線は次の4つの区間に分割される.
が0になるのは,-1,0と1である.そこで,これらの点を数直線上に白抜きまるで印を付ける. これにより,数直線は次の4つの区間に分割される.
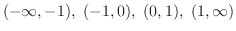
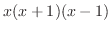 の符号(sgn)は変わらない.
の符号(sgn)は変わらない.
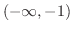 |
![${\rm sgn}[x(x+1)(x-1)] = (-)(-)(-) = -$](img1069.png) |
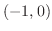 |
![${\rm sgn}[x(x+1)(x-1)] = (-)(+)(-) = +$](img1071.png) |
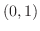 |
![${\rm sgn}[x(x+1)(x-1)] = (+)(+)(-) = -$](img1072.png) |
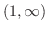 |
![${\rm sgn}[x(x+1)(x-1)] = (+)(+)(+) = +$](img1074.png) |
これより,不等式の解は
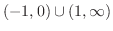 となる.
となる.
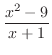 |
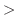 |
0 | |
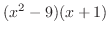 |
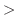 |
0 | |
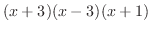 |
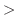 |
0 |
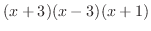 が0になるのは,-3,-1と3である.そこで,これらの点を数直線上に白抜きまるで印を付ける. これにより,数直線は次の4つの区間に分割される.
が0になるのは,-3,-1と3である.そこで,これらの点を数直線上に白抜きまるで印を付ける. これにより,数直線は次の4つの区間に分割される.
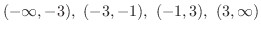
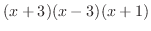 の符号(sgn)は変わらない.
の符号(sgn)は変わらない.
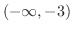 |
![${\rm sgn}[(x+3)(x-3)(x+1)] = (-)(-)(-) = -$](img1083.png) |
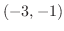 |
![${\rm sgn}[(x+3)(x-3)(x+1)] = (+)(-)(-) = +$](img1085.png) |
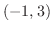 |
![${\rm sgn}[(x+3)(x-3)(x+1)] = (+)(-)(+) = -$](img1086.png) |
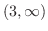 |
![${\rm sgn}[(x+3)(x-3)(x+1)] = (+)(+)(+) = +$](img1088.png) |
これより,不等式の解は
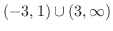 となる.
となる.
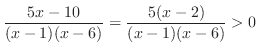
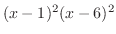 をかけて分母を払う.
をかけて分母を払う.
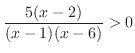 |
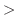 |
0 | |
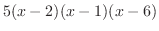 |
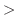 |
0 |
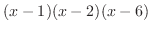 が0になるのは,1,2と6である.そこで,これらの点を数直線上に白抜きまるで印を付ける. これにより,数直線は次の4つの区間に分割される.
が0になるのは,1,2と6である.そこで,これらの点を数直線上に白抜きまるで印を付ける. これにより,数直線は次の4つの区間に分割される.
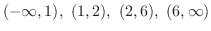
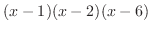 の符号(sgn)は変わらない.
の符号(sgn)は変わらない.
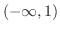 |
![${\rm sgn}[(x-1)(x-2)(x-6)] = (-)(-)(-) = -$](img1096.png) |
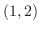 |
![${\rm sgn}[(x-1)(x-2)(x-6)] = (+)(-)(-) = +$](img1097.png) |
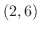 |
![${\rm sgn}[(x-1)(x-2)(x-6)] = (+)(+)(-) = -$](img1099.png) |
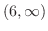 |
![${\rm sgn}[(x-1)(x-2)(x-6)] = (+)(+)(+) = +$](img1101.png) |
これより,不等式の解は
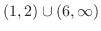 となる.
となる.
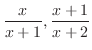
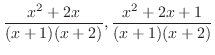
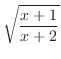 のほうが大きい.
のほうが大きい.
3.
(b)
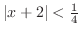 とは,
とは,
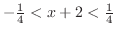 のことである.これより,
のことである.これより,
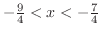 .したがって,不等式の解は
.したがって,不等式の解は
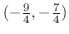
(c)
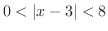 とは,
とは,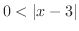 かつ
かつ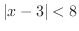 のことである.
のことである.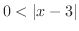 とは
とは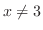 のことである.また,
のことである.また,
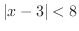 とは,
とは,
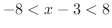 ,つまり,
,つまり,
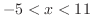 のことである.これより,
のことである.これより,
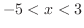 または
または
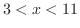 となる.したがって,不等式の解は
となる.したがって,不等式の解は
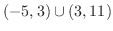
(d)
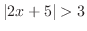 とは,
とは,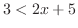 または
または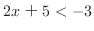 のことである.
のことである.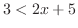 を解くと
を解くと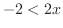 より
より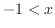 となる.また,
となる.また,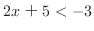 を解くと,
を解くと,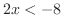 より
より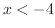 となる,したがって,不等式の解は
となる,したがって,不等式の解は