Next: 3.8 解答 Up: 演習問題詳解 Previous: 3.6 解答 索引
3.7
1.
微分積分学の基本定理は次のように使う.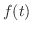 が
が![$[a,b]$](img515.png) で連続で,
で連続で,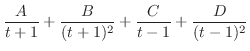 ならば
ならば
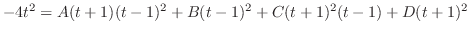
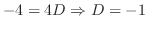
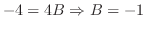
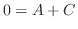 |
 |
![$\displaystyle \frac{d}{dx}[\int_{x}^{a}f(t)\ dt + \int_{a}^{x+1}f(t)\ dt]$](img3751.png) |
|
 |
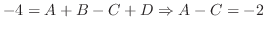 |
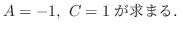 |
 |
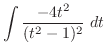 |
|
 |
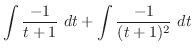 |
||
 |
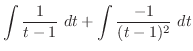 |
2. 定積分は次のようにして求める.
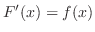 のとき,つまり
のとき,つまり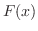 が
が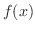 の原始関数であるとき
の原始関数であるとき
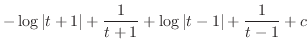
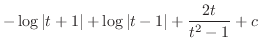
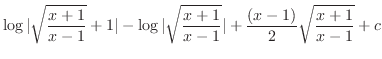 とおくと
とおくと
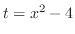 となるので
となるので
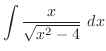
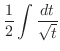
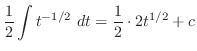 |
 |
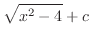 |
|
 |
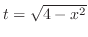 |
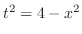 |
 |
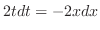 |
|
 |
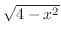 |
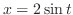 |
 |
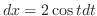 |
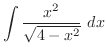
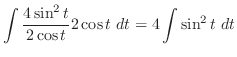 |
 |
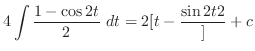 |
|
 |
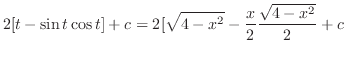 |
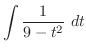
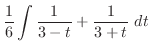 |
 |
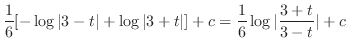 |
|
 |
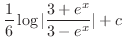 |
3.
4.
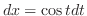
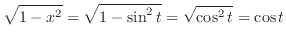 より
より
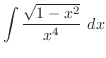
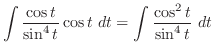
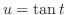
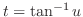
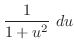
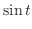
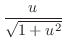
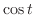
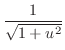
5.
定積分と和の極限値の関係は次の式で与えられる.
区間![$[a,b]$](img515.png) 上で定義された関数
上で定義された関数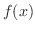 の積分は,区間
の積分は,区間![$[a,b]$](img515.png) を幅
を幅
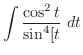 の小区間で刻んでいくと,そこに生まれる長方形の面積(ただし
の小区間で刻んでいくと,そこに生まれる長方形の面積(ただし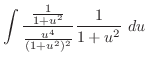 )は
)は
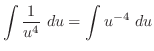
 で収束する定数を次のように表わす.
で収束する定数を次のように表わす.
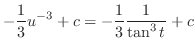
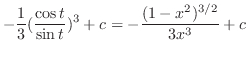 と考えて,次のように求める方が簡単である.
と考えて,次のように求める方が簡単である.
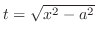
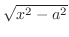 |
 |
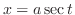 |
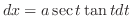 より
より
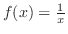 であることが分かる.したがって,
であることが分かる.したがって,
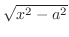 |
 |
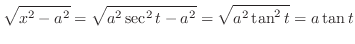 |
|
 |
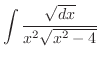 |
別解
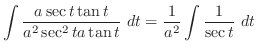 より
より
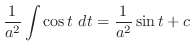 となるので
となるので
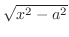 |
 |
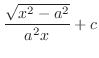 |
|
 |
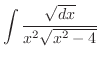 |
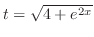 |
 |
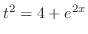 |
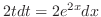 より
より
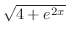 であることが分かる.したがって,
であることが分かる.したがって,
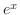 |
 |
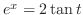 |
|
 |
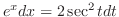 |
||
 |
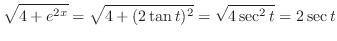 |
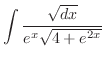 |
 |
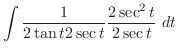 |
|
 |
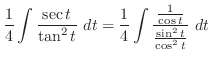 |
||
 |
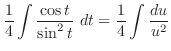 |