Next: 3.5 解答 Up: 演習問題詳解 Previous: 3.3 解答 索引
3.4
1.
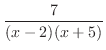 は有理関数で分子の次数
は有理関数で分子の次数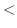 分母の次数なので,部分分数分解すると,
分母の次数なので,部分分数分解すると,
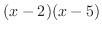 の因数
の因数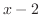 と
と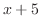 を分母に持つ分数の和で表せる.
を分母に持つ分数の和で表せる.
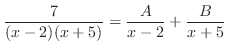
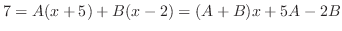
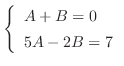
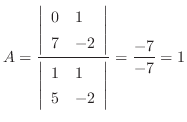
これをもとの式に代入すると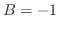 となるので
となるので
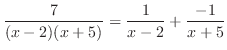
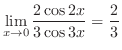
(b)
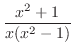 は有理関数で分子の次数
は有理関数で分子の次数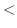 分母の次数なので,部分分数分解すると,
分母の次数なので,部分分数分解すると,
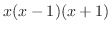 の因数
の因数
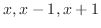 を分母に持つ分数の和で表せる.
を分母に持つ分数の和で表せる.
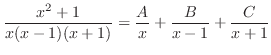
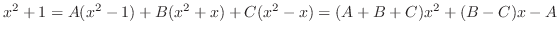
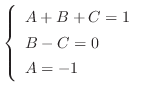
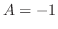 より次の連立方程式を得る.
より次の連立方程式を得る.
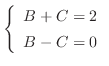
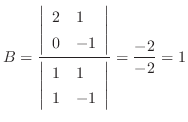
これを上の式に代入すると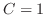 となるので
となるので
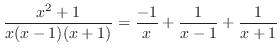
 |
 |
 |
|
 |
 |
(c)
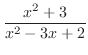 は有理関数で,分子の次数が分母の次数以上なので,まず分子を分母で割ると
は有理関数で,分子の次数が分母の次数以上なので,まず分子を分母で割ると
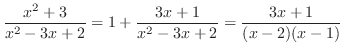
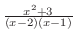 を部分分数分解すると,
を部分分数分解すると,
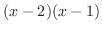 の因数
の因数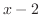 と
と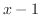 を分母に持つ分数の和で表せる.
を分母に持つ分数の和で表せる.
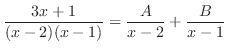
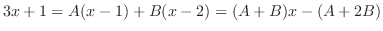
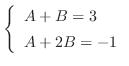
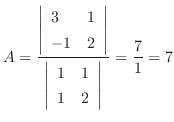
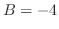 となるので
となるので
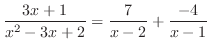
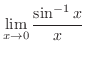 |
 |
 |
|
 |
 |
(d)
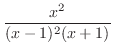 は有理関数で分子の次数
は有理関数で分子の次数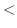 分母の次数なので,部分分数分解すると,
分母の次数なので,部分分数分解すると,
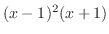 の因数
の因数
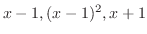 を分母に持つ分数の和で表せる.
を分母に持つ分数の和で表せる.
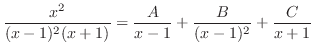
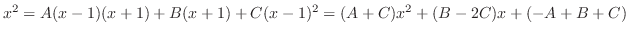
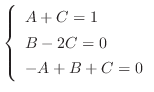
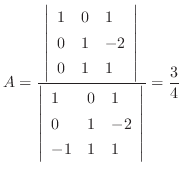
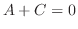 代入すると
代入すると
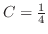 .さらに,
.さらに,
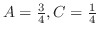 より
より
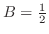 を得る.よって
を得る.よって
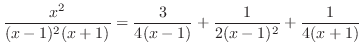
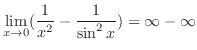 |
 |
 |
|
 |
 |
(e)
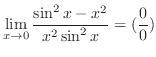 は有理関数で分子の次数
は有理関数で分子の次数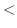 分母の次数なので,部分分数分解をして解く問題と思えるが,分子が定数ということは,これ以上の部分分数分解ができない.実際
分母の次数なので,部分分数分解をして解く問題と思えるが,分子が定数ということは,これ以上の部分分数分解ができない.実際
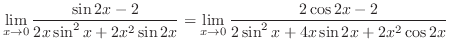
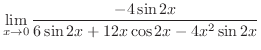
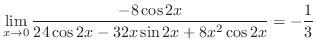
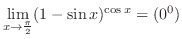 となり,もとに戻ってしまう.
となり,もとに戻ってしまう.
そこで
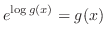 とおき,部分積分を行なう.
とおき,部分積分を行なう.
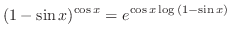
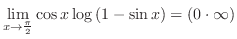 |
 |
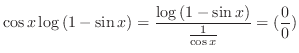 |
|
 |
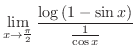 |
||
 |
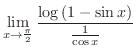 |
||
 |
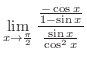 |
![$\displaystyle I_{2} = \frac{1}{32}[\frac{x}{(x^2 + 16)} + I_{1}] = \frac{1}{128}[\frac{4x}{(x^2 + 16)} + \tan^{-1}(\frac{x}{4})] + c$](img3341.png)
別解 (三角関数の積分) この問題は分母が2乗の和で与えられていることに注意すると,
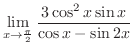 の置換により
の置換により
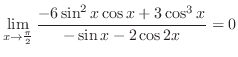
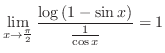 |
 |
 |
|
 |
 |
||
 |
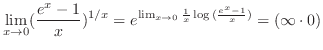 |
||
 |
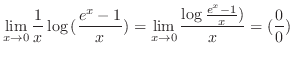 |
(f)
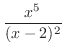 は有理関数で分子の次数
は有理関数で分子の次数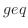 分母の次数なので,まず,分子を分母で割ると,
分母の次数なので,まず,分子を分母で割ると,
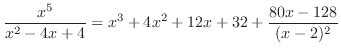
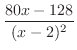 を部分分数分解すると,
を部分分数分解すると,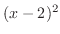 の因数
の因数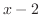 と
と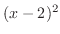 を分母に持つ分数の和で表せる.
を分母に持つ分数の和で表せる.
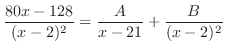
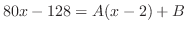
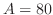 を得る.これを上の式に代入すると,
を得る.これを上の式に代入すると,
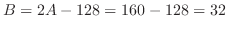 を得る.よって
を得る.よって
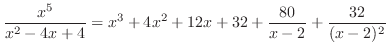
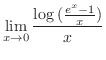 |
 |
 |
|
 |
 |
 |
 |
 |
|
 |
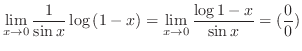 |
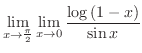
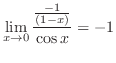
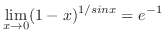
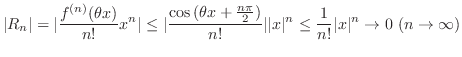 となるので,
となるので,
 |
 |
 |
|
 |
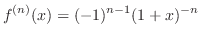 |
||
 |
 |
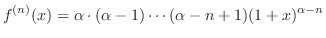 を次のように分解し積分する.
を次のように分解し積分する.
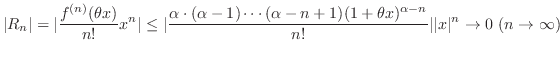 |
 |
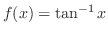 |
|
 |
![$\displaystyle -\frac{1}{2}\int{\frac{2t + 1 -3 }{t^2 + t+1}}dt = -\frac{1}{2}[\...
...ac{2t + 1}{t^2 + t+1}}dt + \int\frac{-3 }{(t + \frac{1}{2})^2 + \frac{3}{4}}dt]$](img3367.png) |
||
 |
![$\displaystyle -\frac{1}{2}[\log\vert t^2 + t+1\vert -3 \frac{2}{\sqrt{3}}\tan^{-1}{(\frac{2(t+\frac{1}{2})}{\sqrt{3}})}]$](img3368.png) |
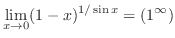 |
 |
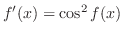 |
|
 |
![$\displaystyle \frac{1}{9}\log\vert t-1\vert + \frac{1}{9}(-\frac{1}{2})[\log\ve...
...t+1\vert -3 \frac{2}{\sqrt{3}}\tan^{-1}{(\frac{2(t+\frac{1}{2})}{\sqrt{3}})}]+c$](img3370.png) |
||
![$\displaystyle \frac{1}{9}\log\vert x^3 -1\vert - \frac{1}{18}[\log\vert x^6 + x^3 + 1\vert + 2\sqrt{3} \tan^{-1}{(\frac{2x^3+1}{\sqrt{3}})}]+c$](img3371.png) |
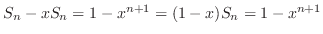 |
 |
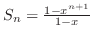 |
|
 |
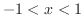 |
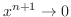
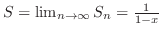
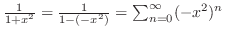
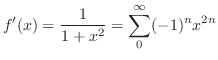 となるので,
となるので,
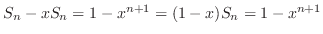 |
 |
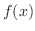 |
|
 |
![$\displaystyle \frac{1}{4}[\log\vert t\vert - \log\vert t+1\vert] + c$](img3382.png) |
||
 |
![$\displaystyle \frac{1}{4}[\log\vert x^4\vert - \log\vert x^4+1\vert] + c = \frac{1}{4}\log{\vert\frac{x^{4}}{x^{4} + 1}\vert} + c$](img3383.png) |