Next: 7.3 変数変換 Up: 確認問題詳解 Previous: 7.1 2重積分 索引
1.
![\begin{figure}\includegraphics[width=4cm]{CALCFIG/ren7-2-1a.eps}
\end{figure}](img2571.png)
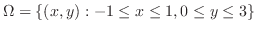
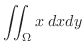 |
 |
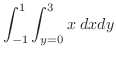 |
|
 |
![$\displaystyle \int_{-1}^{1}\left[xy\right]_{0}^{3}\; dx$](img2575.png) |
||
 |
![$\displaystyle \int_{-1}^{1}3x\; dx = \left[\frac{3x^2}{2}\right]_{-1}^{1} = 0$](img2576.png) |
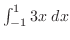 をわざわざ計算したが,
をわざわざ計算したが,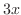 が奇関数であることに気付けば,計算しなくても0であることが分かる.
が奇関数であることに気付けば,計算しなくても0であることが分かる.
![\begin{figure}\includegraphics[width=4cm]{CALCFIG/ren7-2-1b.eps}
\end{figure}](img2579.png)
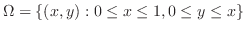
 |
 |
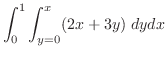 |
|
 |
![$\displaystyle \int_{0}^{1}\left[2xy + \frac{3y^2}{2}\right]_{0}^{x}\; dx$](img2582.png) |
||
 |
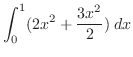 |
||
 |
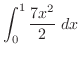 |
||
 |
![$\displaystyle \left[\frac{7}{6}x^3\right]_{0}^{1} = \frac{7}{6}$](img2585.png) |
![\begin{figure}\includegraphics[width=4cm]{CALCFIG/ren7-2-1c.eps}
\end{figure}](img2586.png)
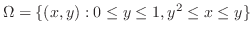
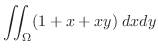 |
 |
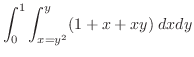 |
|
 |
![$\displaystyle \int_{0}^{1}\left[x + \frac{x^2}{2} + \frac{x^2 y}{2}\right]_{y^2}^{y}\; dy$](img2590.png) |
||
 |
![$\displaystyle \int_{0}^{1}[(y + \frac{y^2}{2} + \frac{y^3}{2}) - (y^2 + \frac{y^4}{2} + \frac{y^5}{2})]\; dy$](img2591.png) |
||
 |
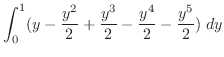 |
||
 |
![$\displaystyle \left[\frac{y^2}{2} - \frac{y^3}{6} + \frac{y^4}{8} - \frac{y^5}{10} - \frac{y^6}{12}\right]_{0}^{1}$](img2593.png) |
||
 |
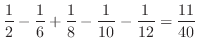 |
![\begin{figure}\includegraphics[width=4cm]{CALCFIG/ren7-2-1d.eps}
\end{figure}](img2595.png)
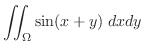 |
 |
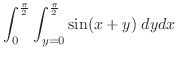 |
|
 |
![$\displaystyle \int_{0}^{\frac{\pi}{2}}\left[-\cos(x+y)\right]_{0}^{\frac{\pi}{2}}\; dx$](img2599.png) |
||
 |
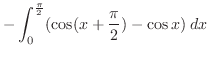 |
||
 |
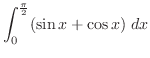 |
||
 |
![$\displaystyle \left[-\cos x + \sin x \right]_{0}^{\frac{\pi}{2}}$](img2602.png) |
||
 |
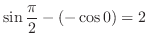 |
![\begin{figure}\includegraphics[width=4cm]{CALCFIG/ren7-2-1b.eps}
\end{figure}](img2579.png)
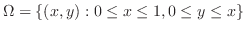
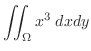 |
 |
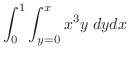 |
|
 |
![$\displaystyle \int_{0}^{1}\left[\frac{x^{3} y^{2}}{2}\right]_{0}^{x}\; dx$](img2606.png) |
||
 |
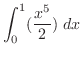 |
||
 |
![$\displaystyle \left[\frac{x^6}{12} \right]_{0}^{1} = \frac{1}{12}$](img2608.png) |
2.
![\begin{figure}\includegraphics[width=4cm]{CALCFIG/ren7-2-2a.eps}
\end{figure}](img2609.png)
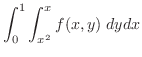 は縦線集合として,累次積分が作られているので,これを横線集合として行なえばよい.
は縦線集合として,累次積分が作られているので,これを横線集合として行なえばよい.
まず,横線は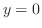 から
から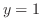 まで引けるので,
まで引けるので,
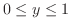 が決まる.そして,小さなブロックを左端から右端まで積むので,左端の曲線の式を求めると,
が決まる.そして,小さなブロックを左端から右端まで積むので,左端の曲線の式を求めると,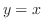 より,
より,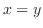 となる.また,右端の曲線の式は
となる.また,右端の曲線の式は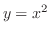 より,
より,
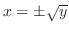 となるが,
となるが, は正であるから,
は正であるから,
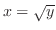 となる.これより,
となる.これより,
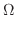 |
 |
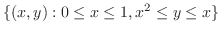 |
|
 |
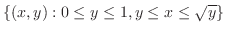 |
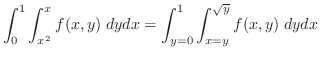
![\begin{figure}\includegraphics[width=4cm]{CALCFIG/ren7-2-2b.eps}
\end{figure}](img2620.png)
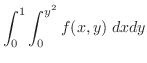 は横線集合として,累次積分が作られているので,これを縦線集合として行なえばよい.
は横線集合として,累次積分が作られているので,これを縦線集合として行なえばよい.
まず,縦線は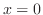 から
から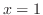 まで引けるので,
まで引けるので,
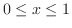 が決まる.そして,小さなブロックを下端から上端まで積むので,下端の曲線の式を求めると,
が決まる.そして,小さなブロックを下端から上端まで積むので,下端の曲線の式を求めると,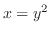 より,
より,
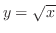 となる.また,上端の曲線の式は
となる.また,上端の曲線の式は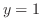 .これより,
.これより,
 |
 |
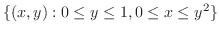 |
|
 |
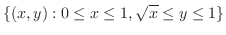 |
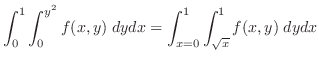
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren7-2-2c.eps}
\end{figure}](img2627.png)
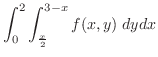 は縦線集合として,累次積分が作られているので,これを横線集合として行なえばよい.
は縦線集合として,累次積分が作られているので,これを横線集合として行なえばよい.
まず,横線は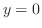 から
から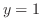 までと
までと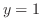 から
から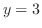 までとで,右端の曲線が異なる.そこで,まず,
までとで,右端の曲線が異なる.そこで,まず,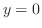 から
から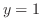 までの領域を表すと,左端の曲線は
までの領域を表すと,左端の曲線は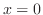 で右端の曲線の式は
で右端の曲線の式は
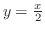 より,
より,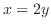 となる.これより,
となる.これより,
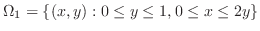
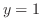 から
から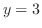 までの領域を表す.左端の曲線は
までの領域を表す.左端の曲線は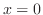 で右端の曲線の式は
で右端の曲線の式は
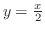 より,
より,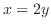 となる.これより,
となる.これより,
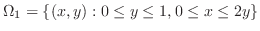
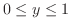 が決まる.そして,小さなブロックを左端から右端まで積むので,左端の曲線の式を求めると,
が決まる.そして,小さなブロックを左端から右端まで積むので,左端の曲線の式を求めると,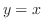 より,
より,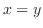 となる.また,右端の曲線の式は
となる.また,右端の曲線の式は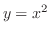 より,
より,
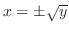 となるが,
となるが, は正であるから,
は正であるから,
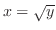 となる.これより,
となる.これより,
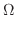 |
 |
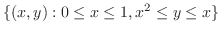 |
|
 |
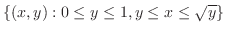 |
3.
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren7-2-3a.eps}
\end{figure}](img2632.png)
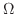 を縦線集合で表すと,
を縦線集合で表すと,
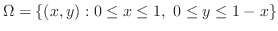 となる.これより,求める体積は,
となる.これより,求める体積は,
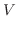 |
 |
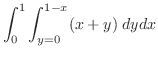 |
|
 |
![$\displaystyle \int_{0}^{1}\left[xy + \frac{y^2}{2}\right]_{0}^{1-x}\; dx$](img2636.png) |
||
 |
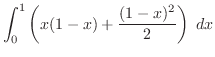 |
||
 |
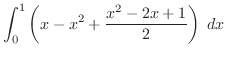 |
||
 |
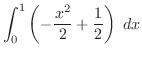 |
||
 |
![$\displaystyle \frac{1}{2}\left[-\frac{x^3}{3} + x\right]_{0}^{1} = \frac{1}{2}\left(-\frac{1}{3} + 1\right) = \frac{1}{3}$](img2640.png) |
(b)
領域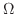 を縦線集合で表すと,
を縦線集合で表すと,
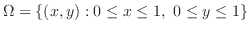 となる.これより,求める体積は,
となる.これより,求める体積は,
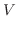 |
 |
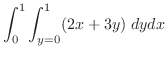 |
|
 |
![$\displaystyle \int_{0}^{1}\left[2xy + \frac{3y^2}{2}\right]_{0}^{1}\; dx$](img2643.png) |
||
 |
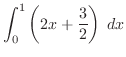 |
||
 |
![$\displaystyle \left[x^2 + \frac{3x}{2}\right]_{0}^{1} = 1 + \frac{3}{2} = \frac{5}{2}$](img2645.png) |
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren7-2-3c.eps}
\end{figure}](img2646.png)
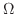 は円なので,極座標で表すと,
は円なので,極座標で表すと,
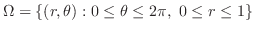 となる.これより,求める体積は,
となる.これより,求める体積は,
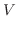 |
 |
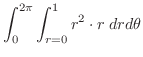 |
|
 |
![$\displaystyle \int_{0}^{2\pi}\left[\frac{r^4}{4}\right]_{0}^{1}\; dx$](img2649.png) |
||
 |
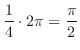 |