順列・組み合わせ

数理統計演習問題 1

1. 0 から 6 までの7個の数字を取り出して並べるとき，次のような4けたの整数はいくつあるか求めよう．

(a)

すべての数字が異なる場合

(b)

5の倍数

(c)

同じ数字が重複してもよい場合

2. 1から10までの番号のついたカードから6枚を取り出すとき，次のような場合の数を求めよう．

(a)

すべての場合

(b)

1と2のカードを含む場合

(c)

1または2のカードを含む場合

3. 1枚の硬貨を5回投げるとき，次の場合は何通りあるか求めよう．

(a)

表の出る回数が0回，1回，2回，3回，4回，5回のそれぞれの場合

(b)

起こりえるすべての場合

4. $a,b,c,d,e,f$の文字を一列に並べるのに次の場合は何通りあるか求めよう．

(a)

$a,b$が隣あう場合

(b)

$a,b$が隣合わない場合

(c)

$a,b$が両端にくる場合

5. $a,a,a,a,b,b,c,d$の8個の文字を並べる順列の総数は ${8 \choose 4,2,1,1}$で与えられることを示せ．

問題解答

1

(a) ここでは $\square \square \square \square$の$\square$の中に異なる数字を入れて4桁の数字を何個作れるか考えてみます．まず，4桁の数字なので，千の位の$\square$には0を使うことができません．そこで千の位は1から6までの6個の中から1個選ぶことになるので，6通り．百の位から一の位までは0から6までのどの数字も使うことができます．しかし，数字を取り出して並べるため，同じ数字は2度使えないことに注意して下さい．では並べてみましょう．

まず，百の位には千の位で用いられた数字以外どれでも使えるので，6通りあります．十の位は千の位と百の位で用いられた数字以外どれでも使えるので，5通りあります．最後に一の位は千の位，百の位，十の位で用いられたもの以外すべて使えるので4通り．よって全部で

$$6\cdot6\cdot5\cdot4 = 720$$

個の4桁の数字を作ることができます．

ここで百の位，十の位，一の位は千の位で用いられた数字以外どれでも1回づつ使うことができることに注意すると，6個の中から3個を取り出し順序をつけて並べる順列の数になるので ${}_6 P_{3}$と表わせます．よって

$$6\cdot {}_6 P_{3} = 6\cdot6\cdot5\cdot4 = 720$$

(b) まず，5の倍数は一の位が必ず，0か5になることに注意します．次に，一の位が0の場合と5の場合を別々に考えます．

一の位が0の場合．

千の位，百の位，十の位は1から6までの数字を1回づつ使うことができるので，6個の中から3個を取り出し並べる順列の数になるので ${}_6 P_{3}$と表わせます．よって 120通り

一の位が5の場合．

千の位に0が使えないので，千の位は0，5以外の5通り，百と十の位は一と千の位で用いた数字以外どれでも1回づつ使えるので${}_5P_{2}$通り．よって $5\cdot {}_5P_{2} = 5\cdot 5 \cdot 4 = 100$通り

ここで，一の位が0の場合と5の場合は同時におきないので，全部で

$$120 + 100 = 220$$   通り$$$$

(c) 同じ数字が重複してもよいので，千の位は1から6までの6通り，百の位は0から6までの7通り，十の位も0から6までの7通り，最後に一の位も0から6までの7通り．したがって，

$$6\cdot {}_7 \Pi_{3} = 6 \cdot 7 \cdot 7 \cdot 7 = 2058$$   通り

2

(a) 1から10までの番号のついたカードから6枚を取り出すとき，何通りの取り出し方があるかを考えます．このとき，一枚づつ順に取り出し並べるわけではないので，取り出す順序を考える必要はありません．よって，何通りの組み合わせがあるかを考えればよいでしょう．

10個の中から6個を取り出す組み合わせは ${}_{10} C_{6}$なので，

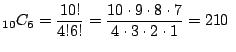$${}_{10} C_{6} = \frac{10!}{4! 6!} = \frac{10 \cdot 9 \cdot 8 \cdot 7 }{4 \cdot 3\cdot 2\cdot 1} = 210$$   通り

(b) 1と2のカードを含むとは取り出した6枚の中に必ず1と2のカードが入っていなければならないということです．

これは1と2を先に引いておいて残りの4枚を3から10までの8枚から選ぶ選び方と考えることができます．よって ${}_8 C_{4} = 70$通り．

(c) 1のカードを含む場合を$C_{1}$，2のカードを含む場合を$C_{2}$とします．すると$C_{1}$は ${}_9 C_{5}$通り，$C_{2}$も ${}_9 C_{5}$通りとなるので，1または2を含む場合は

$${}_9 C_{5} + {}_9 C_{5} - 70 = 252 - 70 = 182$$   通り$$$$

別解 1または2のカードを含むの否定は1と2のカードを含まないとなるので，1と2のカードを含まない場合を考えます．

1と2を含まないので残りの8枚のカードから6枚を取り出すことになるので，その取り出し方は ${}_8 C_{6}$通り．よって，1または2のカードを含む場合は

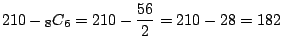$$210 - {}_8 C_{6} = 210 - \frac{56}{2} = 210 - 28 = 182$$   通り$$$$

3

(a) $A_{i} = [表の出る回数がi回]$とおきます．すると表は5回中$i$回どこで出てもよく出る順序は関係ないので，その組み合わせは ${}_5 C_{i}$となります．

$A_{0}$は ${}_5 C_{0} = 1$通り，$A_{1}$は ${}_5 C_{1} = 5$通り，$A_{2}$は ${}_5 C_{2} = 10$通り，$A_{3}$は ${}_5 C_{3} = 10$通り， $A_{4}$は ${}_5 C_{4} = 5$通り，$A_{5}$は ${}_5 C_{5} = 1$通り

(b) 起こりえるすべての場合は ${}_2 \Pi_{5} = 2^5 = 32$通り．または，

$$1 + 5 + 10 + 10 + 5 + 1 = 32$$   通り

4

(a) $a,b$が隣り合うので，$a,b$の順に並んでいるのを$A$とおくと，この問題は5文字を一列に並べる並べ方は何通りあるかという問題と同じになります．したがって，

$${}_5 P_{5} = 5! = 120$$

また，$b,a$の順に並んでいるのを$B$とおくと，

$${}_5 P_{5} = 5! = 120$$

したがって，全部で240通り．

(b) $a,b$が隣り合わないのはすべての並び方から$a,b$が隣り合う場合を引いたもの．よって

$$6! - 240 = 720 - 240 = 480$$   通り$$$$

(c) $a,b$が両端にくるのは$a,b$と$b,a$の場合があることに注意すると，中の4文字の並び方は ${}_4 P_{4}$通りとなるので，全部で

$$2 \cdot {}_4 P_{4} = 2 \cdot 4! = 48$$   通り$$$$

5 ${8 \choose 4,2,1,1} = \frac{8!}{4! 2! 1! 1!}$． 全てに番号をつけて並べると， ${}_8 P_{8} = 8!$通りの並べかたがある．しかし，実際は4個の$a$の重複 ${}_4 P_{4} = 4!$，2個の$b$の重複 ${}_2 P_{2} = 2!$は区別できないので，その組み合わせは $\frac{8!}{4! 2! 1! 1!}$である．