Next: レイアウト Up: シミュレーション Previous: モンテカルロ法 目次 索引
乱数とはある有限の範囲の数の集合から無作為に(ランダムに)選んだ数である。例えばコインを投げて表がでた場合に0,裏の場合には1と決定する目は乱数である。
乱数は一般にモンテカルロシミュレーションに使われるほか,暗号の分野では暗号鍵に決定や初期ベクトル設定,あるいは零知識証明プロトコルにおけるメッセージ生成に用いられる。無作為に選出された数を利用することにより,シミュレーション結果の信頼性や,暗号プロトコルの安全性を保証しているのである。
しかし,ここで発生させる乱数は上で述べた乱数ではない。C++にあるrand()関数により発生する乱数は次のような方法で発生させている。
簡単で実用的な乱数は
ここでは,乱数の応用としてモンテカルロ法を用いた![]() の計算を行う。
の計算を行う。
実際に行うことが困難な実験をコンピュータを用いて模擬的に実験することをシミュレーションという。乱数を用いてシミュレーションを行うことをモンテカルロ法という。このモンテカルロ法を用いてπの計算を行う。
![]() 軸と
軸と![]() 軸,
軸,
![]() の線に囲まれた正方形の中に、ランダムに
の線に囲まれた正方形の中に、ランダムに![]() 個の点
個の点![]() を発生させて、4分の1円の内側に落ちた数を
を発生させて、4分の1円の内側に落ちた数を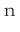 とすると、
とすると、![]() が大きければ
が大きければ

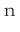 個を数えれば、上式より
個を数えれば、上式より乱数の発生 乱数を発生させるにはrand()関数を用いる。
rand()とすると、1からRAND_MAXまでの数をランダムに発生することができる。ただし,このままではいつも同じ数を発生する。そこで,
srand((unsigned) time(NULL));
とすると,時間によって種(seed)がことなり,rand()で発生する数が変わる。time()関数は![]() ctime
ctime![]() にある。
にある。