next up previous contents index
Next: C言語のプログラム Up: 関数の編集 Previous: ダイアログにユーザ関数を組み込む   目次   索引

最大公約数の基礎知識

２つの数の最大公約数は，ユークリッドの互助法を用いる方法がすばやく結果を出すことで知られている。例えば，316575と7191180の最大公約数(gcd)を求めることを考えてみよう。まず，316575を7191180で割ると割れないので，あまりが316575となる。これを

$\displaystyle 316575\%7191180 = 316575$

と表す。ここで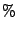，$ \%$は整数での除算におけるあまりを表す。次に，7191180をあまり316575で割ると，あまりが226530となる。このステップをあまりが零になるまで繰り返す方法をユークリッドの互助法という。
$\displaystyle 316575$ $\displaystyle =$ $\displaystyle 0 \times 7191180 + 316575$  
$\displaystyle 7191180$ $\displaystyle =$ $\displaystyle 22 \times 316575 + 226530$  
$\displaystyle 316575$ $\displaystyle =$ $\displaystyle 1 \times 226530 + 90045$  
$\displaystyle 226530$ $\displaystyle =$ $\displaystyle 2 \times 90045 + 46440$  
$\displaystyle 90045$ $\displaystyle =$ $\displaystyle 1 \times 46440 + 43605$  
$\displaystyle 46440$ $\displaystyle =$ $\displaystyle 1 \times 43605 + 2835$  
$\displaystyle 43605$ $\displaystyle =$ $\displaystyle 15 \times 2835 + 1080$  
$\displaystyle 2835$ $\displaystyle =$ $\displaystyle 2 \times 1080 + 675$  
$\displaystyle 1080$ $\displaystyle =$ $\displaystyle 1 \times 675 + 405$  
$\displaystyle 675$ $\displaystyle =$ $\displaystyle 1 \times 405 + 270$  
$\displaystyle 405$ $\displaystyle =$ $\displaystyle 1 \times 270 + 135$  
$\displaystyle 270$ $\displaystyle =$ $\displaystyle 2 \times 135 + 0$  

これより，135は上の全ての式の両辺を割ることができ，かつ，そのような性質持つ数の中で最大の数である。よって，316575と7191180の最大公約数は135となる。

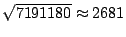ちなみにこの問題を篩い法を用いて素因数分解を行って最大公約数を求めようとすると， $ \sqrt{7191180} \approx 2681$までの素数をチェックしなければならず，その数およそ390個となる。

next up previous contents index
Next: C言語のプログラム Up: 関数の編集 Previous: ダイアログにユーザ関数を組み込む   目次   索引