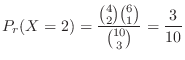Next: Gamma disttribution Up: Theoretical distribution Previous: Normal distribution Contents
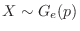 , show
, show
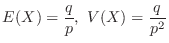
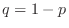 .
.
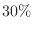 . On average, find out how many games you need to play to win for the first time.
. On average, find out how many games you need to play to win for the first time.
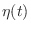 |
 |
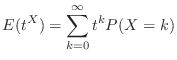 |
|
 |
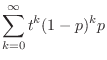 |
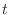 .
.
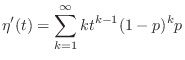
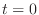 . Then
. Then
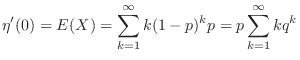
Let
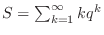 . Then find
. Then find
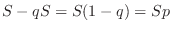
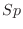 |
 |
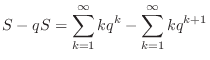 |
|
 |
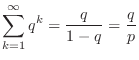 |
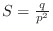 and
and
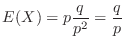
(b) Let 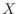 be the numbr of games to play to win the first time. Then
be the numbr of games to play to win the first time. Then
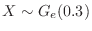 .Thus the number of games to play to win the first time is
.Thus the number of games to play to win the first time is 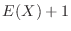
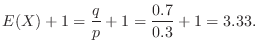
(c) If 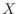 is the number of winning lottery,
is the number of winning lottery,
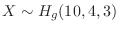 . Therefore, if you draw 3 lots, the probability of winning 2 of them is
. Therefore, if you draw 3 lots, the probability of winning 2 of them is