Next: Poisson distribution Up: Theoretical distribution Previous: Theoretical distribution Contents
1. For the binomial distribution
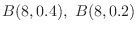 , find the probability disribution.
, find the probability disribution.
2. Suppose there are 25 sets of plastic models, 2 of which are missing some parts. When the customer arbitrarily chooses three sets, find the probability that they are all complete sets.
3. It is said that 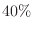 will die within a certain period of time when a certain reagent is injected into a mouse. When the reagent is injected into 8 mice, answer the following questions.
will die within a certain period of time when a certain reagent is injected into a mouse. When the reagent is injected into 8 mice, answer the following questions.
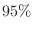 ?
?

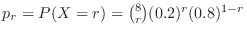 . Then
. Then
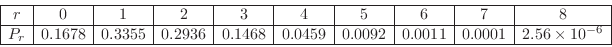
2. The trial to take out the plastic model is Bernoulli trial.
Let 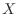 be the number of plastic model sets that are missing parts,Then
be the number of plastic model sets that are missing parts,Then
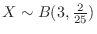 .Thus,the probability that all three selected sets are complete sets is
.Thus,the probability that all three selected sets are complete sets is
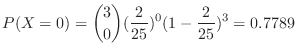
3. Let 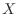 be the number of mice that cannot survive for a certain period of time after injection and die. Then
be the number of mice that cannot survive for a certain period of time after injection and die. Then
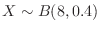 andwe can use the probability distribution obtained in I.
andwe can use the probability distribution obtained in I.
(a) The probability that all eight will survive for a certain period of time is
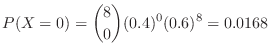
(b) Assuming that 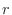 is the number of mice that cannot survive with a probability of
is the number of mice that cannot survive with a probability of 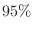 or more, the distribution function
or more, the distribution function 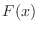 of
of 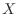 satisfies
satisfies
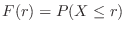 |
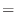 |
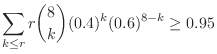 |
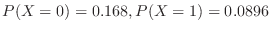 . Then
. Then 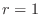 and the number of mice that can survive for
and the number of mice that can survive for 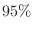 is 7 or more
is 7 or more