Next: Multidimensional probability distribution Up: Random variables Previous: Two-dimensional probability distribution Contents
1. For
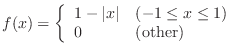
answer the following questions.
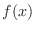 is a probability density function.
is a probability density function.
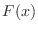 .
.
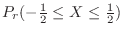 .
.
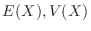 .
.
2. When throwing one dice three times, the number of times a 1 is rolled is 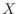 .Then
.Then
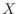 .
.
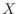 .
.
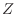 , which is a standardized version of
, which is a standardized version of 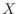 ,Furthermore, find the probability distribution of
,Furthermore, find the probability distribution of 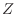 ..
..
3. Find the probability of the followings using Bernoulli's theorem.
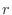 be the number of times the head appears. Then find the probability that
be the number of times the head appears. Then find the probability that
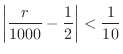
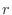 be the number of times the head appears on both coins. Then find the probability that
be the number of times the head appears on both coins. Then find the probability that
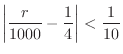
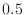 is within
is within 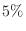 is
is 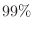 or more.
or more.
(1)
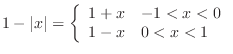
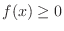 .Also
.Also
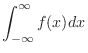 |
 |
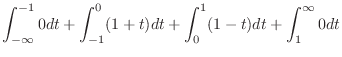 |
|
 |
![$\displaystyle \left[t + \frac{t^2}{2}\right]_{-1}^{0} + \left[t - \frac{t^2}{2}\right]_{0}^{1}$](img246.png) |
||
 |
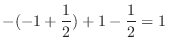 |
For 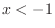 ,
,
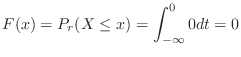
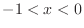 ,
,
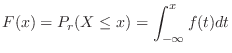 |
 |
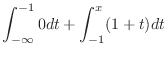 |
|
 |
![$\displaystyle \left[t + \frac{t^2}{2}\right]_{-1}^{x}$](img252.png) |
||
 |
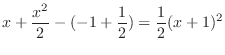 |
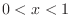 ,,
,,
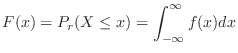 |
 |
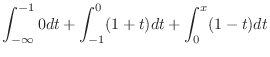 |
|
 |
![$\displaystyle \left[t + \frac{t^2}{2}\right]_{-1}^{0} + \left[t - \frac{t^2}{2}\right]_{0}^{x}$](img256.png) |
||
 |
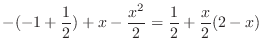 |
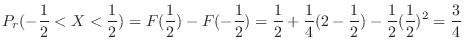
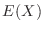 |
 |
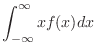 |
|
 |
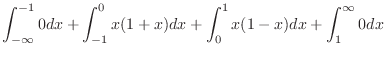 |
||
 |
![$\displaystyle \left[\frac{x^2}{2} + \frac{x^3}{3}\right]_{-1}^{0} + \left[\frac{x^2}{2} - \frac{x^3}{3}\right]_{0}^{1} = 0$](img262.png) |
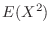 |
 |
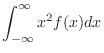 |
|
 |
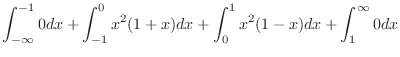 |
||
 |
![$\displaystyle \left[\frac{x^3}{3} + \frac{x^4}{4}\right]_{-1}^{0} + \left[\frac{x^3}{3} - \frac{x^4}{4}\right]_{0}^{1}$](img266.png) |
||
 |
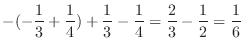 |
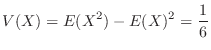
2.
a Let 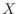 be the number of times 1 is rolled. Then
be the number of times 1 is rolled. Then
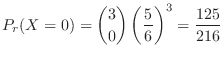
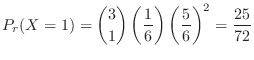
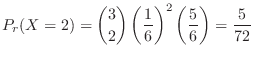
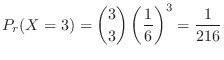
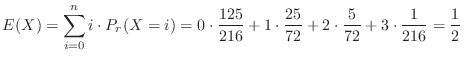
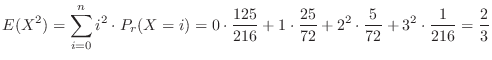
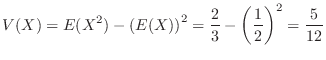
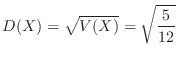
c Standardization of 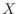 means changing the mean
means changing the mean 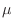 to 0 and the distribution
to 0 and the distribution 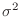 to 1. Then
to 1. Then
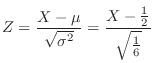
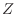 .
.
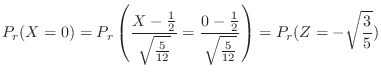
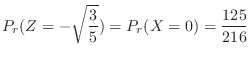
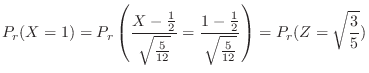
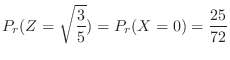
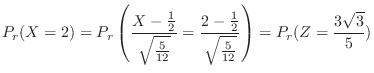
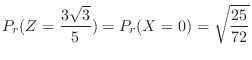
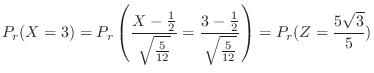
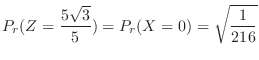
3
a Bernoulli's theorem is when the number of trials is 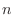 , the number of event occurrences is
, the number of event occurrences is 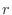 , and the probability of event occurrence is
, and the probability of event occurrence is 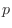 . Then
. Then
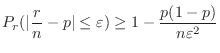
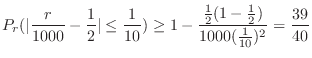
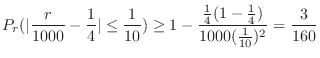
c The problem is to find the probability that the bias of the number of event occurrences 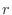 is within 50 when the number of trials is 2000. In other words, find the probability that the error between the percentage of heads appearing in 2000 times
is within 50 when the number of trials is 2000. In other words, find the probability that the error between the percentage of heads appearing in 2000 times
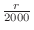 and the theoretical probability
and the theoretical probability
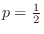 is
is
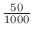 . Then using Bernoulli's theorem,
. Then using Bernoulli's theorem,
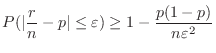
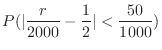 |
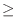 |
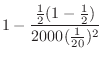 |
|
 |
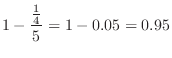 |
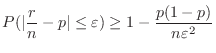
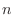 so that
so that
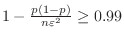 .
.
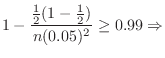 |
|||
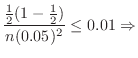 |
|||
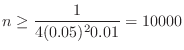 |