Next: Normal distribution Up: Theoretical distribution Previous: Binomial distribution Contents
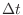 decreases in proportion to
decreases in proportion to 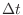 .
.
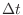 , the probability that the event occurs more than once in the minute time
, the probability that the event occurs more than once in the minute time 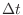 can be ignored..
can be ignored..
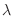 of the event during the time
of the event during the time 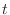 is approximately 5 or less.
is approximately 5 or less.
Let 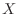 be the number of events that occur in the Poisson process. Then
be the number of events that occur in the Poisson process. Then
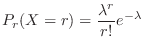
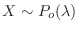 . Here,
. Here, 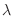 is the average number of events that occur in the Poisson process.
is the average number of events that occur in the Poisson process.
The Poisson process includes scratches on the tape, calls to the switchboard, and broken light bulbs.
1. When the average number of fatalities from traffic accidents is 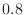 per day, what is the next probability?
per day, what is the next probability?
2.
3.
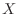 is the number of traffic accidents in a day, the event of traffic accidents is a Poisson process. Therefore, the average number of events in a day
is the number of traffic accidents in a day, the event of traffic accidents is a Poisson process. Therefore, the average number of events in a day 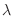 is
is 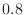 .
.
The day of 0 deaths means finding
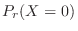 . Thus
. Thus
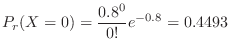
For days with 6 or more deaths,
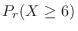 will be calculated. Then
will be calculated. Then
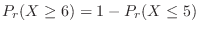
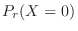 |
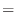 |
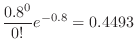 |
|
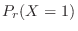 |
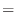 |
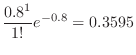 |
|
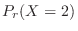 |
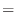 |
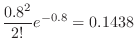 |
|
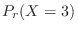 |
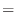 |
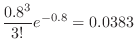 |
|
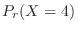 |
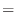 |
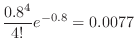 |
|
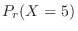 |
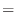 |
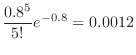 |
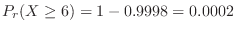
2.
If  is the number of particles emitted from radioactive material per second, the emission of particles is a Poisson process. Therefore, the average number of occurrences of events in one second
is the number of particles emitted from radioactive material per second, the emission of particles is a Poisson process. Therefore, the average number of occurrences of events in one second  is 3. Than this,
The probability that 0 particles will be released per second. Then
SimilarlyC
is 3. Than this,
The probability that 0 particles will be released per second. Then
SimilarlyC
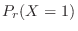 |
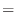 |
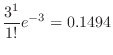 |
|
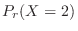 |
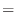 |
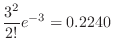 |
|
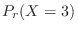 |
 |
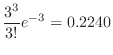 |
|
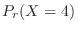 |
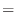 |
 |
|
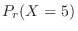 |
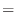 |
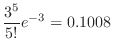 |
|
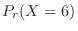 |
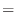 |
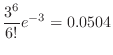 |
Finally, the emission of at least one particle per second is given by
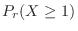 ,
,
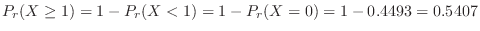
3. If 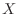 is the number of scratches on the tape, the average number of scratches in 300m is 6, which is
is the number of scratches on the tape, the average number of scratches in 300m is 6, which is
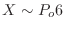 . Therefore, the probability that there will be no scratches in one roll of 300m long tape is
. Therefore, the probability that there will be no scratches in one roll of 300m long tape is