Determinant

Exercise2-8

1. Find the determinant of the following matricex:

(a) $\left \vert \begin{array}{rrr} 2&-3&1\\ 1&0&2\\ 1&-1&1 \end{array}\right\vert$ (b) $\left \vert \begin{array}{rrrr} 2&4&0&5\\ 1&-2&-1&3\\ 1&2&3&0\\ 3&3&-4&-4 \end{array}\right\vert$ (c) $\left \vert \begin{array}{ccccc} 0&0&0&1&0\\ 0&1&0&0&0\\ 0&0&0&0&1\\ 1&0&0&0&0\\ 0&0&1&0&0 \end{array}\right\vert$ (d) $\left\vert\begin{array}{rrrrr} 3 & 5 & 1 & 2 & -1\\ 2 & 6 & 0 & 9 & 1\\ 0 & 0 & 7 & 1 & 2\\ 0 & 0 & 3 & 2 & 5\\ 0 & 0 & 0 & 0 & -6 \end{array}\right\vert$

2. Factor the following matrices:

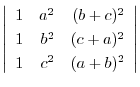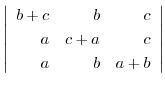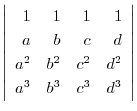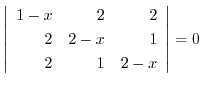
(a) $\left\vert\begin{array}{rrr} 1&a^2&(b+c)^2\\ 1&b^2&(c+a)^2\\ 1&c^2&(a+b)^2 \end{array}\right\vert$ (b) $\left\vert\begin{array}{rrr} b+c&b&c\\ a&c+a&c\\ a&b&a+b \end{array}\right\vert$ (c) $\left\vert\begin{array}{rrrr} 1&1&1&1\\ a & b & c & d\\ a^2 & b^2 & c^2 & d^2\\ a^3 & b^3 & c^3 & d^3 \end{array}\right\vert$ 3. Solve the following equations:． $\left\vert\begin{array}{rrr} 1-x&2&2\\ 2&2-x&1\\ 2&1&2-x \end{array}\right\vert = 0$

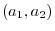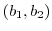4. Show the equation of the straight line going through two points $(a_{1},a_{2})$ and $(b_{1},b_{2})$ is given by

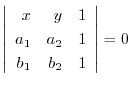
$\displaystyle \left\vert\begin{array}{rrr} x&y&1\\ a_{1}&a_{2}&1\\ b_{1}&b_{2}&1 \end{array}\right\vert = 0$

5. Show the equation of the plane going through 3 points 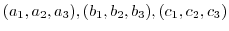$(a_{1},a_{2},a_{3}),(b_{1},b_{2},b_{3}),(c_{1},c_{2},c_{3})$ is given by

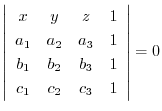
$\displaystyle \left\vert\begin{array}{cccc} x&y&z&1\\ a_{1}&a_{2}&a_{3}&1\\ b_{1}&b_{2}&b_{3}&1\\ c_{1}&c_{2}&c_{3}&1 \end{array}\right\vert = 0$

．

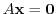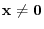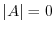6. Suppose that a system of linear equation $A{\mathbf x} = {\bf0}$ has a fundamental solution ${\mathbf x} \neq {\bf0}$ . Then show that $\vert A\vert = 0$ ．

7. Solve the following system of linear equations using Cramer's rule．

(a) $\left\{\begin{array}{rrr} x-3y&=&5\\ 3x-5y&=&7 \end{array}\right .$

(b) $\left\{\begin{array}{rrr} x+y+z&=&3\\ x+2y+2z&=&5\\ x+2y+3z&=&6 \end{array}\right .$