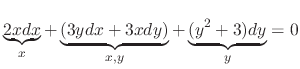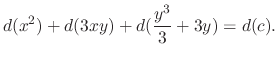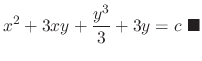Next: Exercise Up: 1st Order Differential Equation Previous: Exercise Contents Index
The total differential of 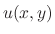 is
is
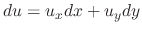
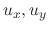 , then we can find
, then we can find 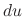 . On the other hand, if we know the total differential
. On the other hand, if we know the total differential 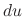 of a function
of a function 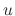 , then we can determine the function
, then we can determine the function 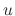 .
.
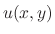 is given by
is given by
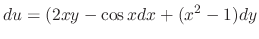
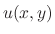 .
.
SOLUTION
Since
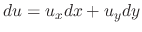 , we have
, we have
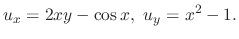
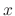 to obtain
to obtain
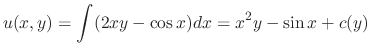
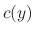 is an arbitrary function of
is an arbitrary function of 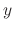 . Now differentiate with respect ot
. Now differentiate with respect ot 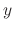 ,
,
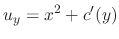
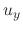 obtained and the
obtained and the 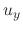 given above must be the same. Thus
given above must be the same. Thus
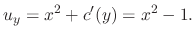
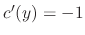 and
and
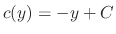 .
Therefore,
.
Therefore,
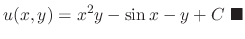
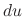 of some function
of some function 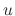 . Then the general solution is given by
. Then the general solution is given by
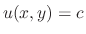
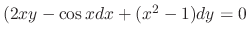 .
.
SOLUTION
In the example above, we found the function 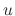 so that
so that 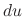 is equal to the left-hand side of equation. Thus the general solution is
is equal to the left-hand side of equation. Thus the general solution is
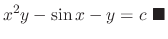
 and
and 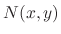 be the class
be the class 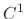 on
on
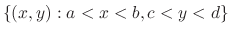 . Then the followings are equivalent
. Then the followings are equivalent
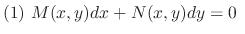 is exact
is exact
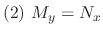
Proof
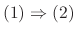
If the differential equation is exact, then there exists 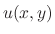 satisying
satisying
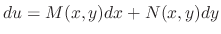 . Thus we have
. Thus we have
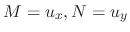
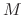 with respect to
with respect to 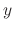 and partially differentiate
and partially differentiate 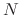 with respect to
with respect to 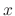 . Then
. Then
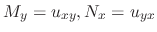
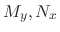 are continuous,
are continuous,
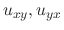 are also continuous.Thus by Schwarz lemma,
are also continuous.Thus by Schwarz lemma,
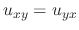 and
and
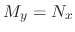 .
.
 be a point in the domain of
be a point in the domain of 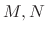 . Consider
. Consider
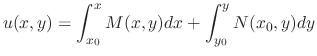
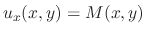 . Since
. Since 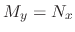 ,
,
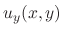 |
 |
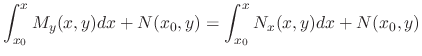 |
|
 |
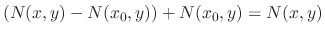 |
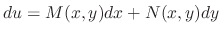
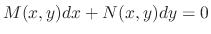 is exact differential equation.
is exact differential equation.

In the proof above, the general solution of 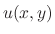 is given.
is given.
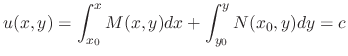
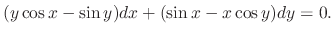
SOLUTION
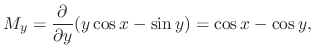
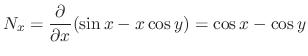
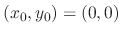 to have
to have
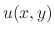 |
 |
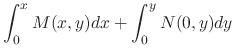 |
|
 |
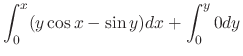 |
||
 |
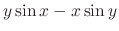 |
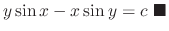
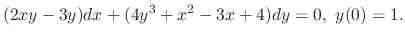
SOLUTION
Note that
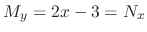 ,
,
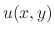 |
 |
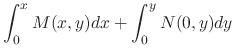 |
|
 |
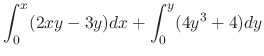 |
||
 |
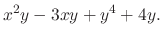 |
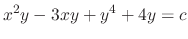
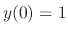 , we have
, we have 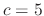

Instead of using the formula
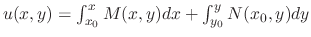 , we introduce a simpler method called grouping method.
, we introduce a simpler method called grouping method.
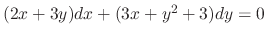 .
.
SOLUTION
Note that
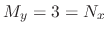 . Thus it is exact. Now we write
. Thus it is exact. Now we write
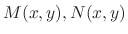 as
as