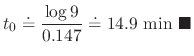Next: Exercise Up: 1st Order Differential Equation Previous: Exercise Contents Index
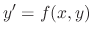
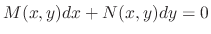
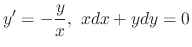
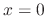 . Thus we formally treat both equations as the same equation.
. Thus we formally treat both equations as the same equation.
If the differential equation
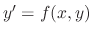 is expressed in the form
is expressed in the form
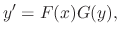
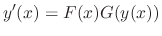
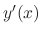 as
as
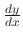 , and then write
, and then write
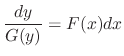
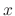 to obtain
to obtain

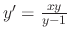 .
.SOLUTION We can rewrite this differential equation as
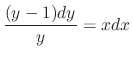
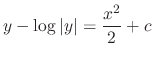
 . Then
. Then
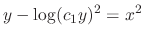
 is a solution. But no matter how you choose
is a solution. But no matter how you choose 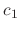 , it is impossible to obtain
, it is impossible to obtain 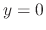 . Thus
. Thus 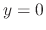 is a singular solution. As we noted above, when we are asked to find the general solution, we solve the differential equation by quadrature. Thus do not worry about a singular solution.
is a singular solution. As we noted above, when we are asked to find the general solution, we solve the differential equation by quadrature. Thus do not worry about a singular solution.
Let 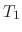 and
and 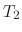 be the temparature of two objects facing each other. Then the heat transfers from warmer body to cooler body in the time
be the temparature of two objects facing each other. Then the heat transfers from warmer body to cooler body in the time  is given by
is given by 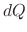 and
and
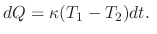 where
where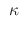 is constant
is constant
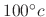 . Then submerge the iron ball into the water whose temparature is kept at
. Then submerge the iron ball into the water whose temparature is kept at
 . After
. After  minutes, the temparature of the iron ball is
minutes, the temparature of the iron ball is
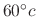 . Find the time when the temparature of the iron ball is
. Find the time when the temparature of the iron ball is
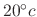 .
. SOLUTION We formulate this problem by using Newton's law of cooling. Then
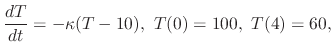
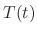 is a temparature of the iron ball after
is a temparature of the iron ball after 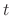 minutes later. Since this differential equation is separable, we obtain
minutes later. Since this differential equation is separable, we obtain
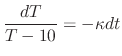
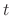 . Then
. Then

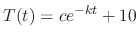
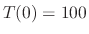 and
and 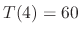 ,
we have
,
we have
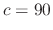 and
and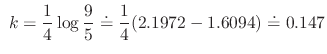
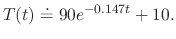
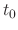 satisfying
satisfying  .
.