Next: Exercise Up: Power series solution of Previous: Power series solution of Contents Index
Let
 be a sequence of functions defined on the interval
be a sequence of functions defined on the interval 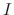 . Then consider the partial sums
. Then consider the partial sums
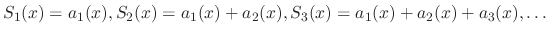
 for all
for all 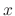 in
in 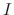 , then we say
, then we say
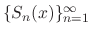 converges and
converges and 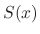 is called the sum of the series .
For all
is called the sum of the series .
For all 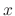 in
in 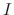 , there exists
, there exists 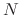 such that
such that
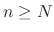 implies
implies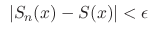
 is called uniformly convergent.
is called uniformly convergent.
Let
 . Then the uniform convergence of the series is expressed as follows:
For each
. Then the uniform convergence of the series is expressed as follows:
For each 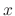 in the interval
in the interval 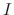 , there exists a number
, there exists a number 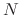 such that
such that
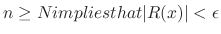 .
.
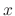 in some interval
in some interval 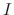 , there exists a sequence of real functions
, there exists a sequence of real functions  satisfying the followings
satisfying the followings
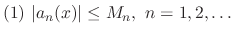

 converges uniformly and absolutely on
converges uniformly and absolutely on 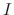 .
.
Proof
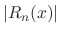 |
 |
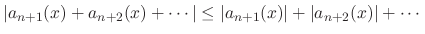 |
|
 |
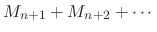 |
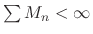 , for all
, for all
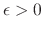 , there exists
, there exists 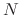 such that
such that  implies
implies
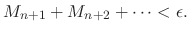
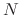 is indepedent of
is indepedent of 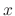 , for
, for 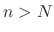 ,
,
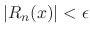

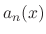 is continuous on the interval
is continuous on the interval 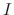 and
and
 converges uniformly on
converges uniformly on 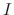 , then
, then
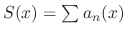 is continuous on
is continuous on  .
.
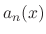 is continuous on the interval
is continuous on the interval 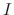 and
and
 is uniformly convergent on
is uniformly convergent on 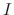 , then
, then
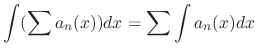
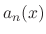 is continuous on the interval
is continuous on the interval 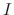 and
and
 is uniformly convergent on
is uniformly convergent on 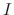 , then
, then

If
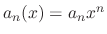 , then the series
, then the series
 is called a power series. For example,
is called a power series. For example,
 |
|||
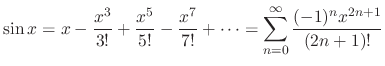 |
|||
 |
|||
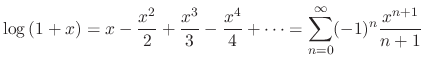 |
Given
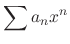 , by the ratio test, if
, by the ratio test, if
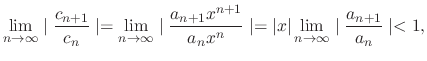
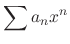 converges. Thus,
if
converges. Thus,
if
 , then
, then
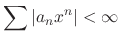
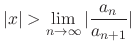 , then
, then
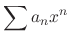 is divergent. Then the limit
is divergent. Then the limit
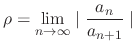
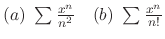
SOLUTION

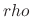 be the radius of convergence of
be the radius of convergence of
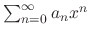 . Suppose that
. Suppose that
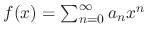 . Then
. Then
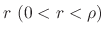 ,
,
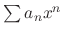 converges uniformly on
converges uniformly on 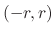 .
.
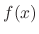 is the class
is the class
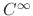 on
on
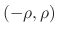 .
.
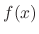 is continuous on
is continuous on
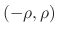 .
.
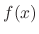 is term-by-term differentiable on
is term-by-term differentiable on
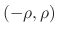 and
and
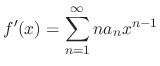
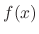 is term-by-term integrable on
is term-by-term integrable on
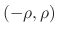 and
and
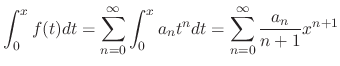
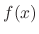 on
on
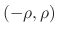 is the same as the power series
is the same as the power series
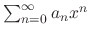 . Thus,
. Thus,
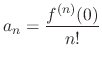
If 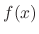 is expressed as the power series of the positive radius
is expressed as the power series of the positive radius
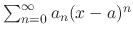 , then
, then 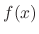 is called analytic at
is called analytic at 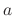 .
.