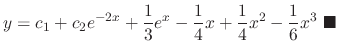Next: Exercise Up: Linear Differential Equations Previous: Exercise Contents Index
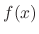 is the solution of the homogeneous linear differential equation. Let
is the solution of the homogeneous linear differential equation. Let
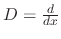 . Then
. Then
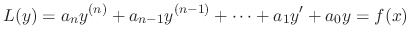
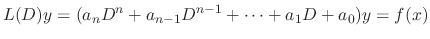
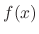 is the solution of the homogeneous linear differential equation, there exists a polynomial
is the solution of the homogeneous linear differential equation, there exists a polynomial  satisfying
satisfying
 .
Let
.
Let 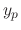 be the particular solution of
be the particular solution of
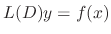 . Then
. Then
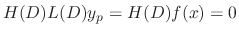
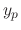 , all we need to find is solutions of
, all we need to find is solutions of
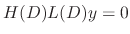 satisfying
satisfying
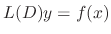 .
This method is called the method of undetermind coefficient.
.
This method is called the method of undetermind coefficient.
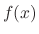 |
 |
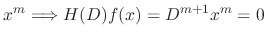 |
|
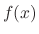 |
 |
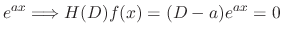 |
|
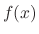 |
 |
 |
|
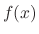 |
 |
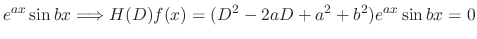 |
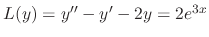 .
.
SOLUTION
The characteristic equation of 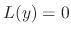 is
is
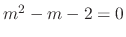 . Then the roots of characteristic equation are
. Then the roots of characteristic equation are 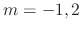 . Then the complementary solution
. Then the complementary solution 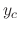 is
is
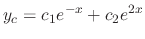
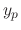 using the method of undetermined coefficients.
Let
using the method of undetermined coefficients.
Let
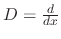 . Then since
. Then since
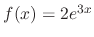 , let
, let
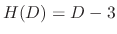 . Then
. Then
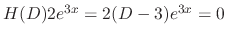 . Thus
. Thus 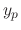 is a solution of
is a solution of
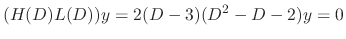
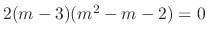 . Thus the fundamental solutions are
. Thus the fundamental solutions are
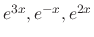 .
Since
.
Since
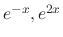 satisfy
satisfy 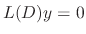 . Thus we set
. Thus we set 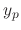 as
as
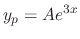
 . Then
. Then

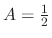 . Thus
. Thus
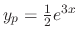 and the general solution is
and the general solution is
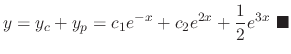
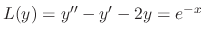 .
.
SOLUTION
The characteristic equation of 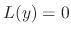 is given by
is given by
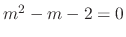 . Thus we have
. Thus we have 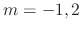 . Then the complementary solution
. Then the complementary solution 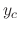 is
is
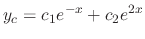
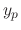 using the method of undetermined coefficients. Since
using the method of undetermined coefficients. Since
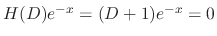 ,
, 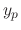 is a solution of
is a solution of

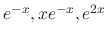 . But
. But
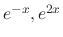 are solution of
are solution of 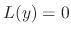 . Thus we set
. Thus we set
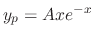
 . Then
. Then
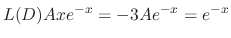
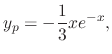
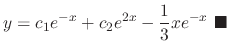
 .
.
SOLUTION
The characteristic equation of 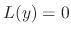 is
is
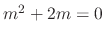 . Then we have
. Then we have  . Thus, the complementary solution
. Thus, the complementary solution 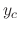 is
is

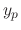 , we find the particular solution
, we find the particular solution 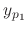 of
of
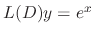 and
and 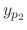 of
of
 . Then
. Then 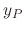 is given by
is given by
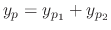 .
.
The particular solution 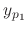 of
of
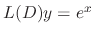 can be found by setting
can be found by setting
 . Also the particular solution
. Also the particular solution 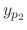 of
of
 can be found by setting
can be found by setting
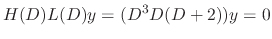
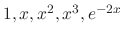 are the fundamental solutions.But
are the fundamental solutions.But 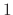 and
and 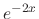 are complementary solutions. Thus set
are complementary solutions. Thus set
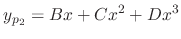
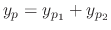 and substitute into
and substitute into
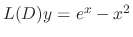 . Then
. Then
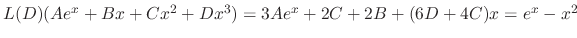 . Thus
. Thus
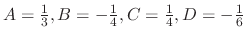 . Therefore, the general solution is
. Therefore, the general solution is