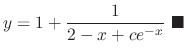Next: Exercise Up: 1st Order Differential Equation Previous: Exercise Contents Index
If a differential equation is written in the form
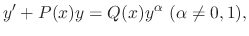
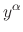 by multiplying
by multiplying
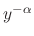 to both sides of equation.
to both sides of equation.
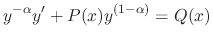
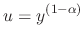
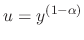 ,
,
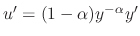 implies
implies
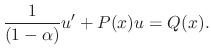
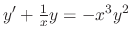 .
.
SOLUTION
This is a Bernoulli's equation. Then multiply 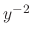 to both sides of equation.
to both sides of equation.
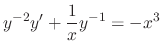
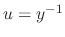 . Then
. Then
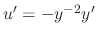 and
and
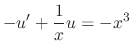
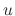 . So, rewrite this into the normal form.
. So, rewrite this into the normal form.
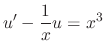
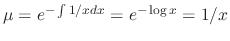 . Multiplying
. Multiplying 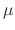 to both sides of the equation and noting the left-hand side becomes the derivative of the integrating factor times the independent variable
to both sides of the equation and noting the left-hand side becomes the derivative of the integrating factor times the independent variable 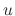 . Thus we have
. Thus we have
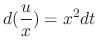
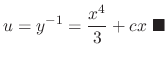
Given
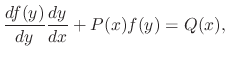
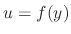 . Then since
. Then since
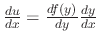 ,
,
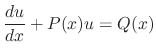
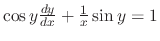 .
.
SOLUTION
Let
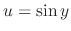 . Then
. Then
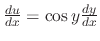 .
Thus the given differential equation is expressed in the form
.
Thus the given differential equation is expressed in the form
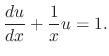
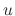 . Then the integrating factor
. Then the integrating factor
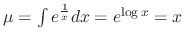 . Now multiply
. Now multiply 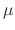 to both sides of the equation to get
to both sides of the equation to get
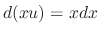
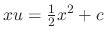 . Solve for
. Solve for 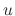 to get
to get
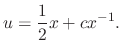
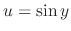 ,
,
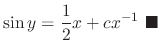
The differential equation expressed in the form
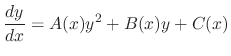
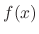 is found, then we let
is found, then we let
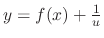 .
Now
.
Now
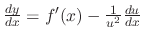 . Thus
. Thus
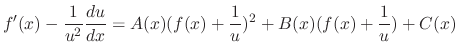
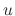 .
.
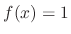 .
.
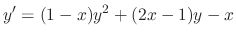
SOLUTION
This is a Riccati's equation. Since 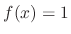 is a solution to the equation. Thus let
is a solution to the equation. Thus let
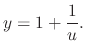
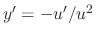 . Substitute this into the differetial equation.
. Substitute this into the differetial equation.
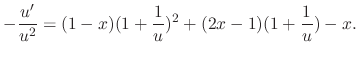
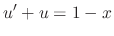
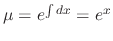 to both sides of the equation to get
to both sides of the equation to get
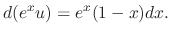
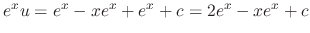
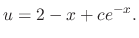
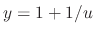 , we have
, we have