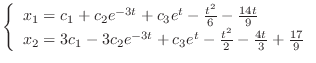Next: Solution by Series Up: System of Linear Differentia Previous: Multiple Roots and Complex 目次 索引
(b)
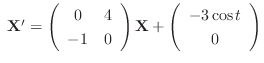
(c)
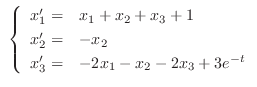
(d)
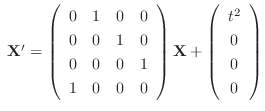
2. Rewrite the following differential equation into the system of linear differential equation. Then solve.
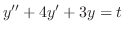
3. Solve the following differential equation using the elimination method.
Answer
1.
(a)
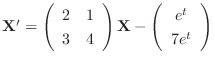 . Then we find the solution
. Then we find the solution  of
of
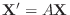 .
.
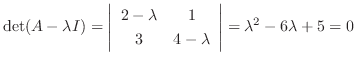
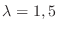 .
.
We find the eigenvector  corresponds to
corresponds to
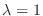 using Gaussian elimination.
using Gaussian elimination.
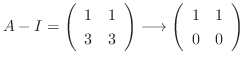
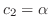 . Then
. Then
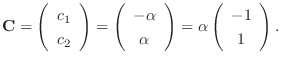
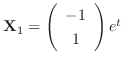 .
.
We find the eigenvector  corresponds to
corresponds to
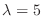 .
.
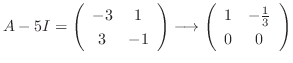
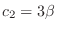 . Then
. Then
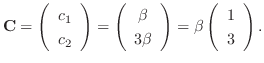
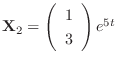 . From this, the fundamental matrix
. From this, the fundamental matrix 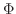 is given by
is given by
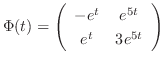
Next we find the particular solution 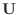 by solving
by solving
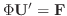 .
.
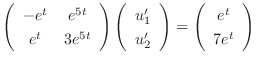
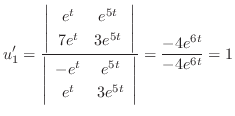
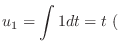 it is particular solution. So, no constanat
it is particular solution. So, no constanat
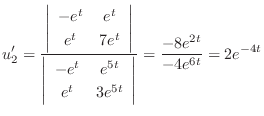
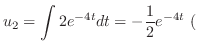 it is particular solution. So, no constant
it is particular solution. So, no constant
 |
 |
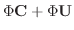 |
|
 |
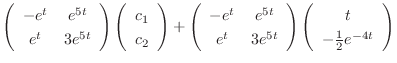 |
(b)
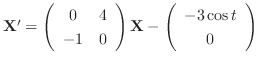 . Then we find the solution
. Then we find the solution 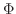 satisfying
satisfying
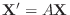 .
.
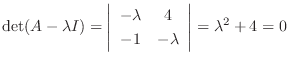
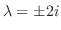 .
.
We find the eigenvector  corresponds to
corresponds to
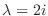 using Gaussian elimination.
using Gaussian elimination.
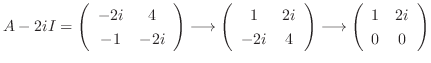
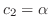 . Then
. Then
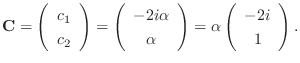
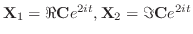 .
.
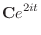 |
 |
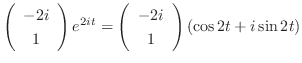 |
|
 |
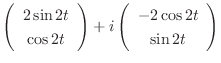 |
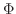 is given by
is given by
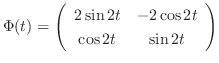
We next find the particular solution 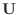 satisfying
satisfying
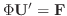 .
.
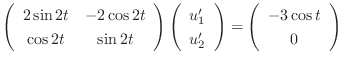
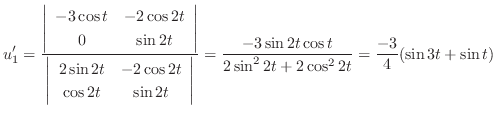
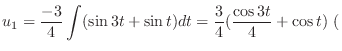 no constant term
no constant term
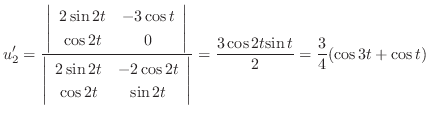
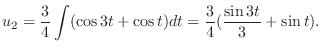
 |
 |
 |
|
 |
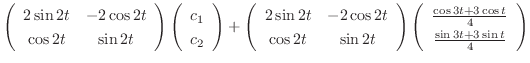 |
(c)
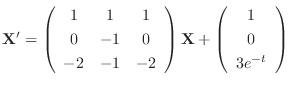 . Then find the solution
. Then find the solution 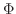 of
of
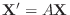 .
.
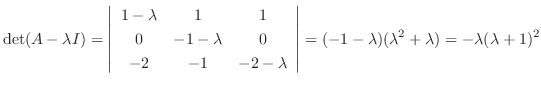
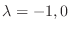 .
.
We find the eigenvector  corresponds to
corresponds to
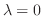 using Gaussian elimination.
using Gaussian elimination.
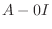 |
 |
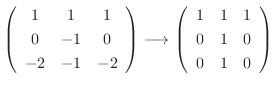 |
|
 |
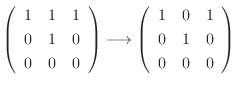 |
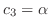 . Then
. Then
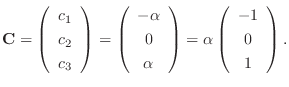
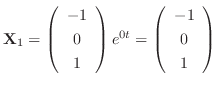 .
.
Find the eigenvector  corresponds to
corresponds to
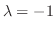 .
.
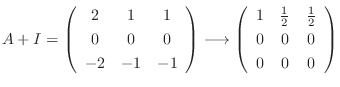
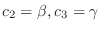 . Then
. Then
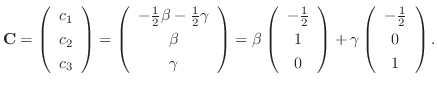
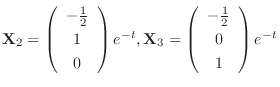 . Thus the fundamental matrix
. Thus the fundamental matrix 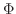 is given by
is given by
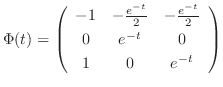
We find the particular solution 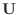 of
of
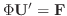 .
.
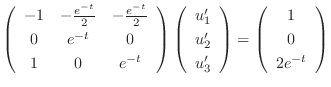
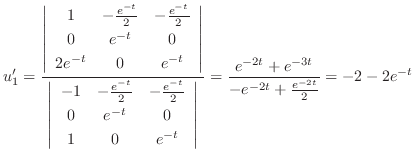
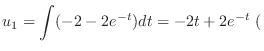 no constant term
no constant term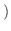
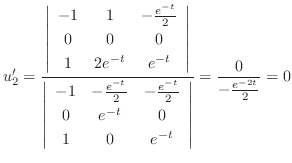
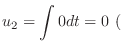 no constant term
no constant term
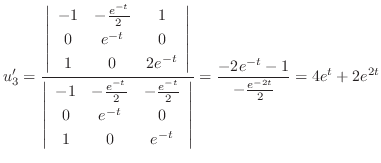
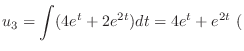 no constant term
no constant term
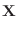 |
 |
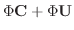 |
|
 |
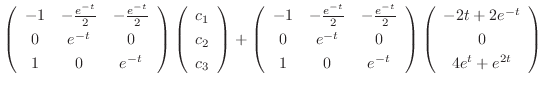 |
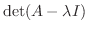 |
 |
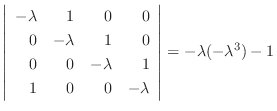 |
|
 |
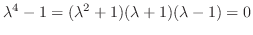 |
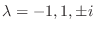 .
.
We find the eigenvector  corresponds to
corresponds to
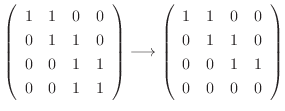
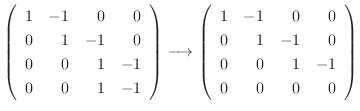
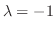 using Gaussian elimination.
using Gaussian elimination.
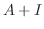 |
 |
 |
|
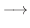 |
 |
||
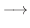 |
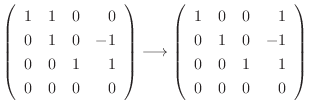 |
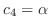 . Then
. Then
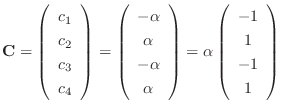
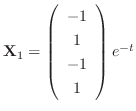 .
.
We find the eigenvector  corresponds to
corresponds to
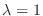 .
.
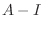 |
 |
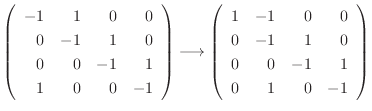 |
|
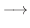 |
 |
||
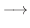 |
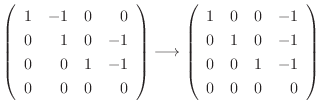 |
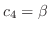 . Then
. Then
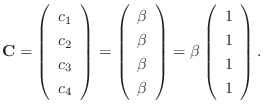
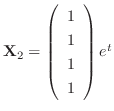 .
.
We find the eigenvector  corresponds to
corresponds to
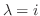 .
.
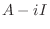 |
 |
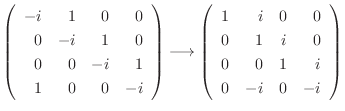 |
|
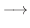 |
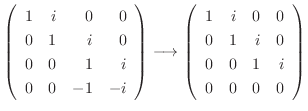 |
||
 |
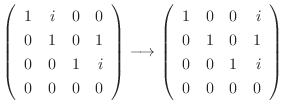 |
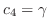 . Then,
. Then,
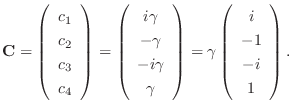
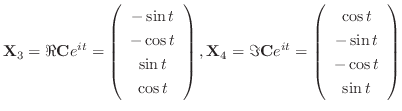
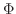 is given by
is given by
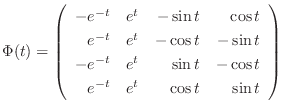
Next we find the particular solution 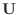 satisfying
satisfying
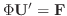 .
.
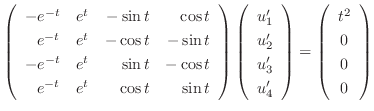
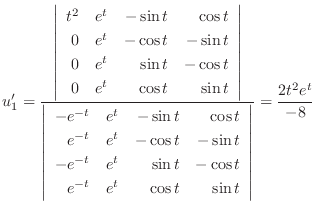
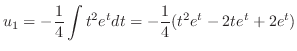
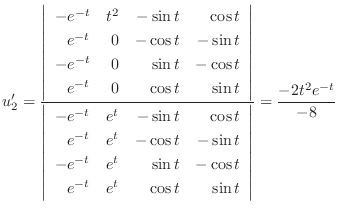
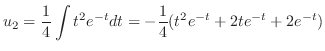
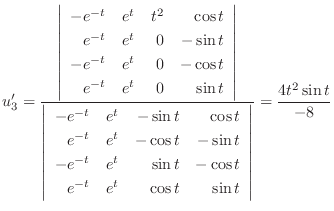
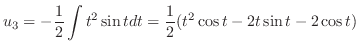
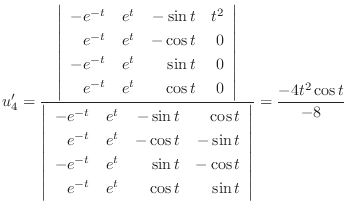
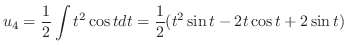
 |
 |
 |
|
 |
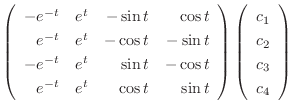 |
||
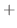 |
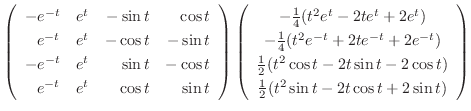 |
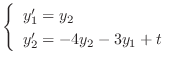
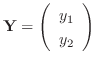 . Then we can write
. Then we can write
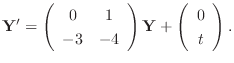
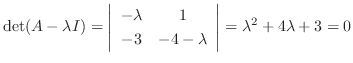
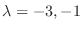 .
.
We find the eigenvector  corresponds to
corresponds to
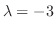 using Gaussian elimination.
using Gaussian elimination.
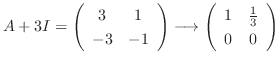
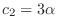 .
.
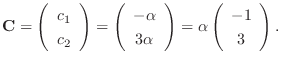
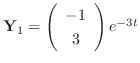 .
.
We find the eigenvector corresponds to
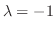 .
.
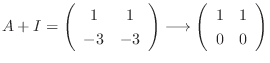
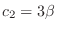 . Then
. Then
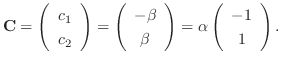
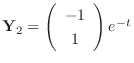 . Thus the fundamental matrix
. Thus the fundamental matrix 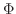 is given by
is given by
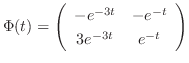
Next we find the particular solution 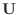 satisfying
satisfying
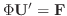 .
.
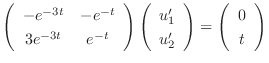
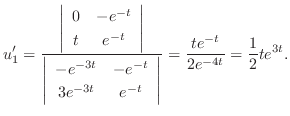
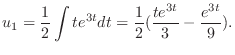
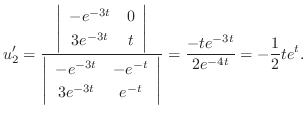
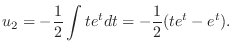
 |
 |
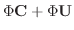 |
|
 |
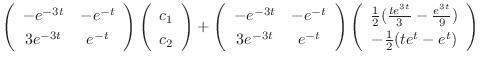 |
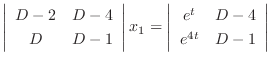
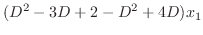 |
 |
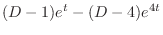 |
|
 |
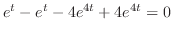 |
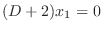
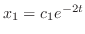 . Similarly, we can find
. Similarly, we can find 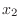 . To find
. To find 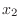 , eliminate
, eliminate 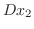 frpm the equation 3.3. Then substitute
frpm the equation 3.3. Then substitute 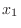 . In fact, subtract the 2nd equation from the 1st equation in 3.3. Then
. In fact, subtract the 2nd equation from the 1st equation in 3.3. Then
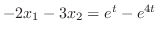 . Thus,
. Thus,
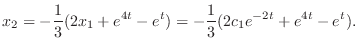
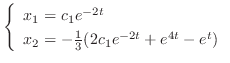
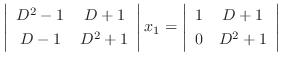
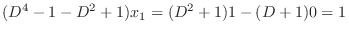
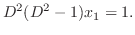
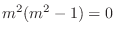 . Then
. Then
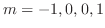 .
Thus , the complementary function is
.
Thus , the complementary function is
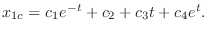
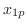 using the method of undetermined coefficient.
using the method of undetermined coefficient.
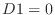 . Then
. Then
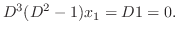
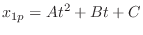
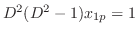 implies that
implies that 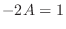 . Thus,
. Thus,
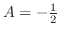 . Therefore,
. Therefore,
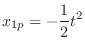
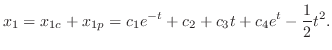
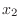 . Eliminate
. Eliminate
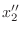 from the equation 3.4. Then
from the equation 3.4. Then
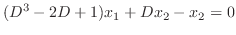
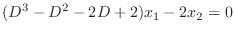
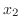 |
 |
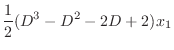 |
|
 |
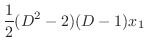 |
||
 |
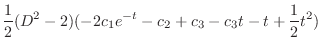 |
||
 |
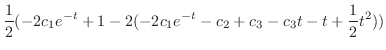 |
||
 |
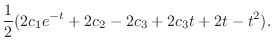 |
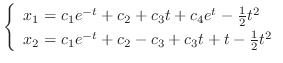
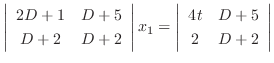
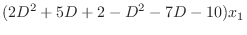 |
 |
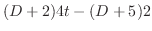 |
|
 |
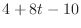 |
||
 |
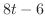 |
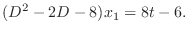
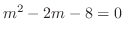 . Then
. Then 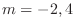 .
Thus the complementary function is
.
Thus the complementary function is
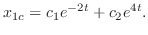
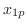 using the method of undermined coefficient.
using the method of undermined coefficient.
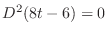 implies
implies
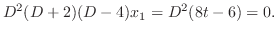
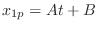
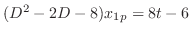 . Thus
. Thus
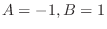 .
.
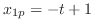
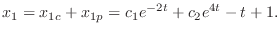
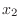 . eliminate
. eliminate
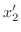 from the equation 3.5. Then we have
from the equation 3.5. Then we have
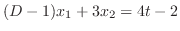
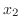 |
 |
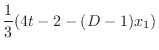 |
|
 |
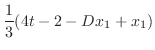 |
||
 |
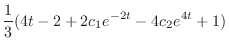 |
||
 |
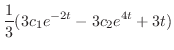 |
||
 |
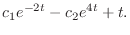 |
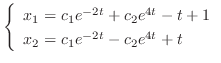
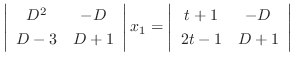
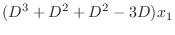 |
 |
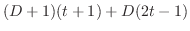 |
|
 |
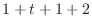 |
||
 |
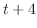 |
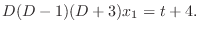
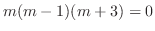 and
and
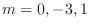 .
Thus, the complementary function is given by
.
Thus, the complementary function is given by
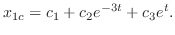
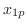 using the mathod of undetermined coefficient.
using the mathod of undetermined coefficient.
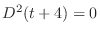 implies
implies
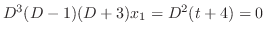 . Note that
. Note that
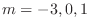 are already used in the complementary function. So we let
are already used in the complementary function. So we let
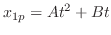
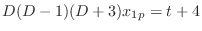 . Thus we have
. Thus we have
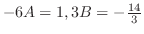 .
Then
.
Then
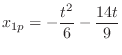
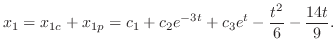
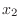 . Eliminate
. Eliminate
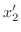 from the equation 3.6. Then we have
from the equation 3.6. Then we have
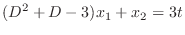
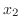 |
 |
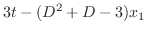 |
|
 |
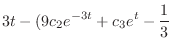 |
||
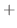 |
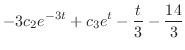 |
||
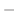 |
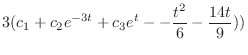 |
||
 |
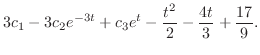 |