Next: Multiple Roots and Complex Up: System of Linear Differentia Previous: System of Linear Differentia 目次 索引
Answer
1.
(a)
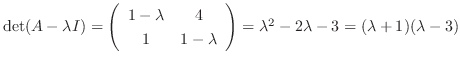 implies that the eigenvalues are
implies that the eigenvalues are
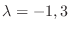 . Then we find the eigenvector
. Then we find the eigenvector 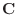 corresponding to
corresponding to
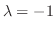 . Note that
. Note that 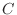 satisfies the follwing equation.
satisfies the follwing equation.
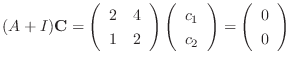
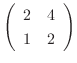 is row reduced to echlon form
is row reduced to echlon form
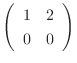 . Then let
. Then let
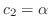 . Then
. Then
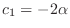 . Therefore, the eigenvector is
. Therefore, the eigenvector is
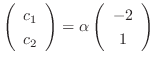 となり,
となり,
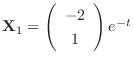 .
.
We next find the eigenvector corresponds to
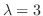 .
.
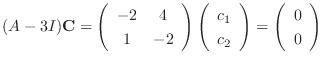
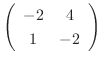 is row reduced echelon form
is row reduced echelon form
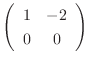 . Now look at the echelon form. no leading one in 2nd row. So, we let
. Now look at the echelon form. no leading one in 2nd row. So, we let
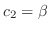 . Then
. Then
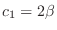 . Therefore, the eigenvector is
. Therefore, the eigenvector is
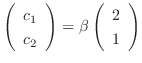 . Thus,
. Thus,
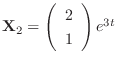 .
Then the general solution is given by
.
Then the general solution is given by
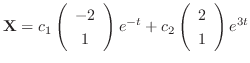
(b)
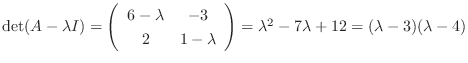 implies that the eigenvalues are
implies that the eigenvalues are
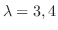 . Then we find the eigenvector C corresponds to
. Then we find the eigenvector C corresponds to
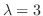 .
. 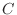 satisfies the following equation.
satisfies the following equation.
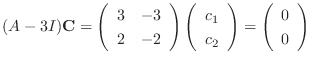
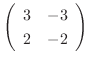 is row reduced to echelon form
is row reduced to echelon form
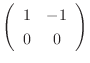 . Now there is no leading one in 2nd row. So we let
. Now there is no leading one in 2nd row. So we let
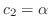 . Then
. Then
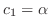 . Therefore, the eigenvector is
. Therefore, the eigenvector is
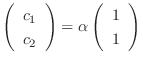 and
and
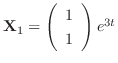 .
.
We next find the eigenvector corresponds to
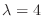 .
.
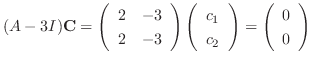
 is row reduced to echelon form
is row reduced to echelon form
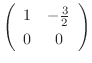 . Then there is no leading one in 2nd row. So, we let
. Then there is no leading one in 2nd row. So, we let
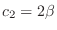 . Then
. Then
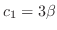 . Thus, the eigenvector is
. Thus, the eigenvector is
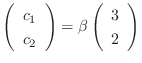 and
and
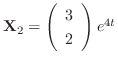 .
Therefore, the general solution is give by
.
Therefore, the general solution is give by
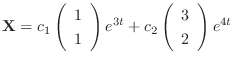
(c)
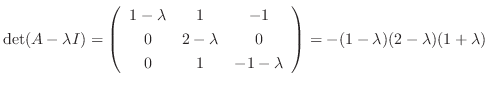 implies that the eigenvalues are
implies that the eigenvalues are
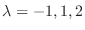 . Then we find the eigenvector
. Then we find the eigenvector 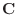 correponds to
correponds to
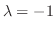 .
. 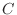 satisfies the following equation.
satisfies the following equation.
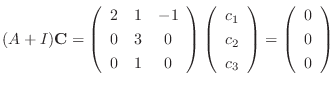
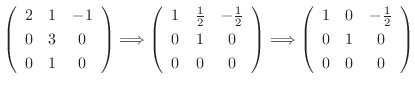
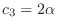 . Then
. Then
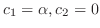 . Thus, the eigenvector is
. Thus, the eigenvector is
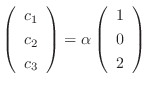 and
and
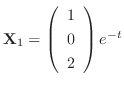 .
.
We next find the eigenvector corresponding to
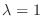 .
.
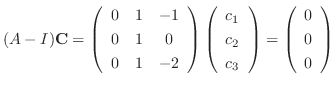
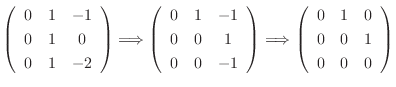
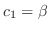 . Then
. Then
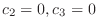 . Thus the eigenvector is
. Thus the eigenvector is
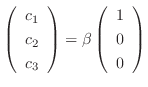 and
and
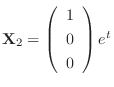 .
.
We find the eigenvector corresponds to
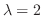 .
.
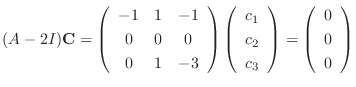
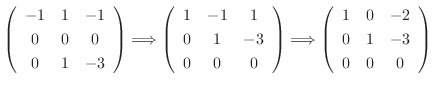
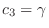 . Then
. Then
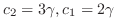 . Thus, the eigenvector is
. Thus, the eigenvector is
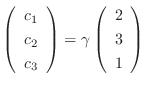 and
and
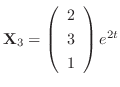 .
.
Therefore, the general solution is given by
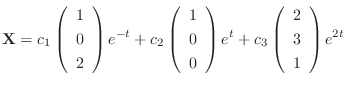
(d)
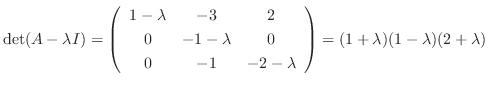 implies that the eigenvalues are
implies that the eigenvalues are
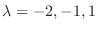 . Then we find the eigenvector
. Then we find the eigenvector 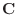 corresponds to
corresponds to
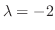 . Note that the eigenvector
. Note that the eigenvector 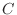 satisfies the following equation.
satisfies the following equation.
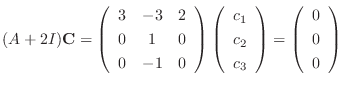
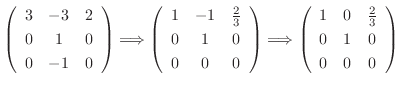
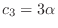 . Then
. Then
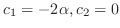 . Thus the eigenvector is
. Thus the eigenvector is
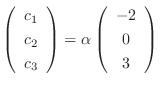 and
and
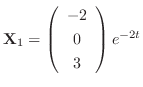 .
.
Next we find the eigenvector corresponding to
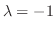
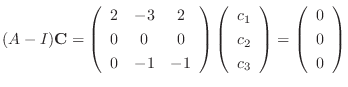
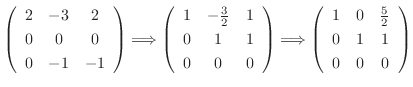
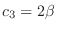 . Then
. Then
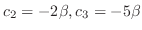 . Thus, the eigenvector is
. Thus, the eigenvector is
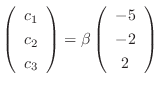 and
and
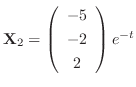 .
.
We find the eigenvector corresponds to
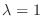 .
.
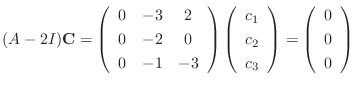
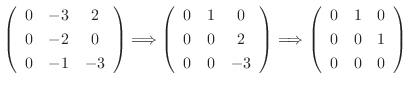
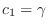 . Then
. Then
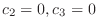 . Thus the eigenvector is
. Thus the eigenvector is
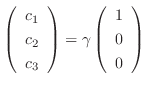 and
and
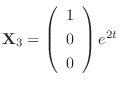 .
.
Therefore the general solution is
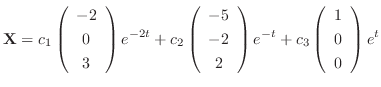
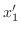 |
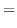 |
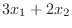 |
|
 |
 |
 |
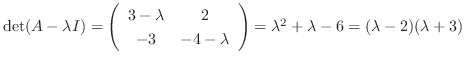 .
This implies that eigenvalues are
.
This implies that eigenvalues are
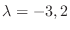 . Then we find the eigenvector
. Then we find the eigenvector 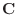 corresponds to
corresponds to
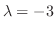
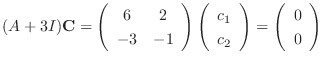
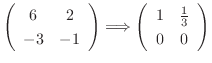
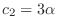 . Then
. Then
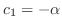 . Thus the eigenvector is
. Thus the eigenvector is
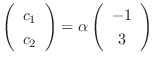 and
and
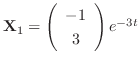 .
.
We next find the eigenvector corresponding to
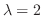 .
.
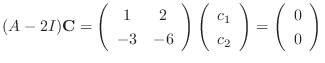
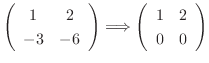
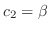 . Then
. Then
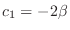 . Thus, the eigenvector is
. Thus, the eigenvector is
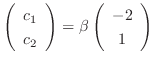 and
and
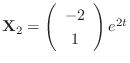 .
THerefore, the general solution is given by
.
THerefore, the general solution is given by
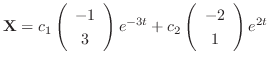
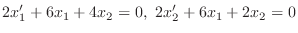
 |
 |
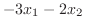 |
|
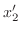 |
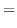 |
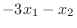 |
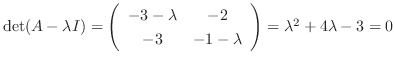 .
Then the eigenvalues are
.
Then the eigenvalues are
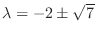 . Now we find the eigenvector
. Now we find the eigenvector 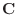 corresponds to
corresponds to
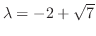 .
Now the matrix
.
Now the matrix
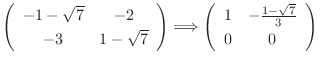 is row reduced echelon form and no leading one in the 2nd row. So, we let
is row reduced echelon form and no leading one in the 2nd row. So, we let
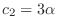 . Then
. Then
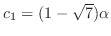 . Thus, the eigenvector is
. Thus, the eigenvector is
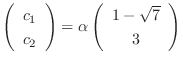 and
and
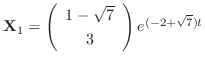 .
.
We next find the eigenvector corresponds to
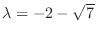 .
The matrix
.
The matrix
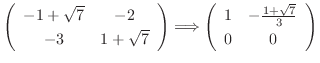 is row reduced echelon form and no leading one in the 2nd row. So, we let
is row reduced echelon form and no leading one in the 2nd row. So, we let
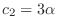 . Thne
. Thne
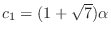 . Thus the eigenvector is
. Thus the eigenvector is
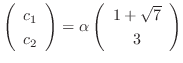 and
and
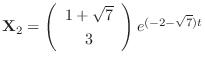 .
.
Therefore, the general solution is given by