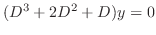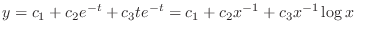Next: System of Linear Differentia Up: Linear Differential Equations Previous: Variation of Parameter 目次 索引
 .
.
Answer
1.
(a) Set
 . Then the indicial equation is
. Then the indicial equation is
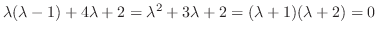
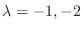 . Note that this indicial equation is the characteristic equation of the following differential equation.
. Note that this indicial equation is the characteristic equation of the following differential equation.
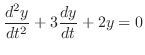
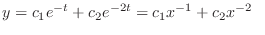
(b) Set
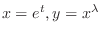 . Then the indicial equation is given by
. Then the indicial equation is given by
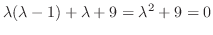
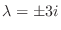 . Note that this indicial equation is the characteristic equation of the following equation.
. Note that this indicial equation is the characteristic equation of the following equation.
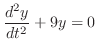
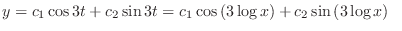
(c) Set
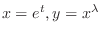 . Then the indicial equation is given by
. Then the indicial equation is given by
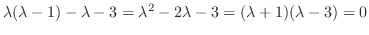
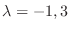 . Note that this indicial equation is the characteristic equation of the following equation.
. Note that this indicial equation is the characteristic equation of the following equation.
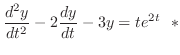
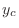 is
is
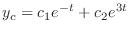
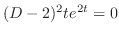 , we have
, we have
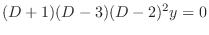
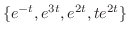 . But
. But
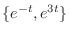 are already used in the
are already used in the 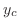 . So, we omit these solutions from
. So, we omit these solutions from 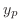 . Then we have
. Then we have
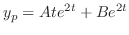
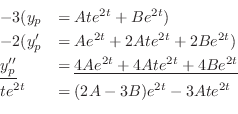
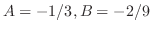 and ,
and ,
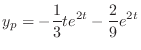
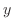 |
 |
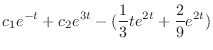 |
|
 |
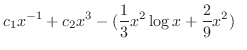 |
(d) Set
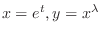 . Then the indicial equation is given by
. Then the indicial equation is given by
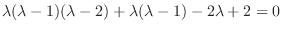
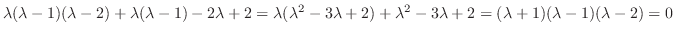
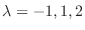 . This indicial equation is the characteristic equation of the following differential equation.
. This indicial equation is the characteristic equation of the following differential equation.
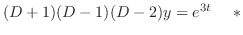
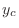 is given by
is given by
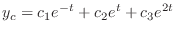
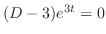 , we have
, we have
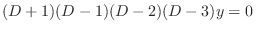
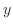 to get
to get
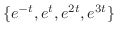 . But
. But
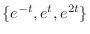 are already used in
are already used in 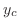 . So, we omit from
. So, we omit from 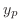 . Then we have
. Then we have
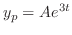
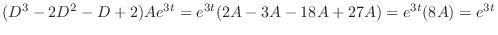
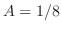 and
and
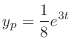
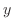 |
 |
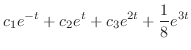 |
|
 |
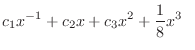 |
(e) Given equation is not Euler's equation. But if we multiply  to both sides. Then it becomes Euler's equation.
to both sides. Then it becomes Euler's equation.
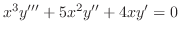
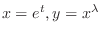 . Then the indicial equation is
. Then the indicial equation is
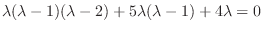
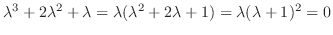
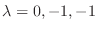 . Not that this indicial equation is th echaracteristic equation of the following differential equation.
. Not that this indicial equation is th echaracteristic equation of the following differential equation.