Next: Exercise Up: 1st Order Differential Equation Previous: Exercise Contents Index
If a 1st order differential equation
 is put into the form
is put into the form


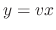 and
and
 . Substitute these into the above equation, we have
. Substitute these into the above equation, we have



 to get the general solution.
to get the general solution.
If a function 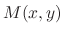 satisfies
satisfies
 , then we say
, then we say 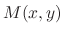 is the homogeneous function of degree
is the homogeneous function of degree 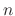 .
.
Given

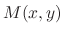 and
and 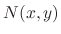 are the homogeneous functions of the same degree, then the differential equation is homogeneous.
are the homogeneous functions of the same degree, then the differential equation is homogeneous.
 .
.
SOLUTION
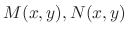 are the homogeneous functions of the same degree 1. Divide the numerator and the denominator by
are the homogeneous functions of the same degree 1. Divide the numerator and the denominator by  . Then
. Then

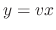 . Then
. Then
 and
and





 as base to get
as base to get


 to obtain the general solution
to obtain the general solution

 .
.SOLUTION This is not homogeneou. But once we can get rid of the constant term, it becomes homogeneous. The intersetion of two lines

 . we move the axis so that
. we move the axis so that  is the origin. Let
is the origin. Let
 . Then
. Then
 and
and



 , we have
, we have

 .
.
SOLUTION
Let  . Then
. Then  and
and
 . Put this back into the original differential equation to obtain
. Put this back into the original differential equation to obtain




