Next: Exercise Up: Power series solution of Previous: Exercise Contents Index
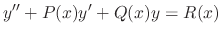
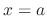 is not an ordinary point, then
is not an ordinary point, then 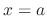 is called a singular point.
For
is called a singular point.
For 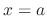 singular point and
singular point and
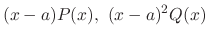
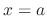 is called a regular singular point. Otherwise, irregular singular point.
is called a regular singular point. Otherwise, irregular singular point.
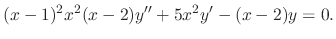
SOLUTION Since
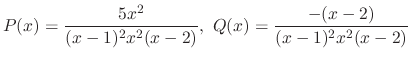
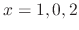 are singular points. Now
are singular points. Now
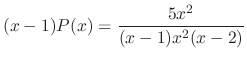
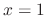 is irregular singular point and the rest is regular singular point.
is irregular singular point and the rest is regular singular point.

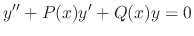
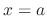 is the regular singular point, then there exists a solution around
is the regular singular point, then there exists a solution around 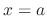 of the form
of the form
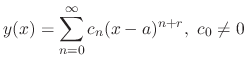
The power series
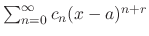 is called Frobinius series. Using the Frobinious series to find
is called Frobinius series. Using the Frobinious series to find 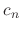 is called Frobenius method.
is called Frobenius method.
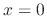 .
.
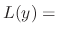
SOLUTION
Write
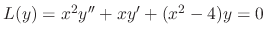 as the standard form
as the standard form
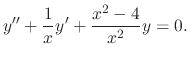
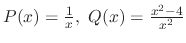 . Thus
. Thus
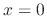 is the regular singular point.
Now we set a solution of the differential equation as
is the regular singular point.
Now we set a solution of the differential equation as
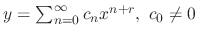 . Differentiate to get
. Differentiate to get
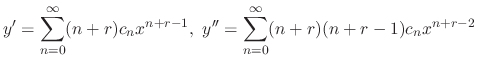
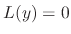 to obtain
to obtain
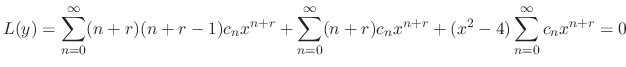
Now let the power of  be the least number
be the least number 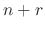 . Then
. Then
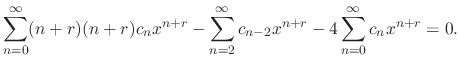
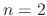
![$\displaystyle \underbrace{(r^2 -4)c_{0}x^{r}}_{n = 0} + \underbrace{((r+1)^2 -4...
...x^{r+1}}_{n = 1} + \sum_{n=2}^{\infty}[((n+r)^2 - 4)c_{n} + c_{n-2}]x^{n+r} = 0$](img1292.png) |
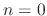 , we have the indicial equation
, we have the indicial equation
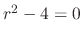 which implies
which implies 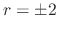 .
.
We find a solution for 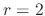 . Note that the coefficients of
. Note that the coefficients of 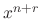 are 0. Thus
are 0. Thus
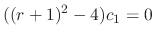
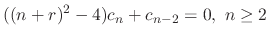
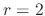 , we have
, we have 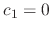 .
Similarly, for
.
Similarly, for 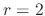 , we have
, we have
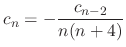
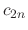 |
 |
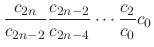 |
|
 |
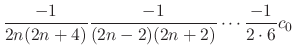 |
||
 |
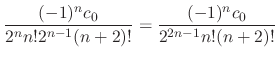 |
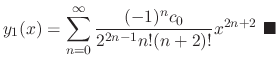
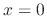 .
.
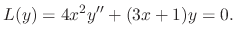
SOLUTION
Write in the standard form. Then since
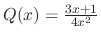 ,
, 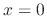 is a regular singular point. We let
is a regular singular point. We let
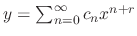 .Then
.Then
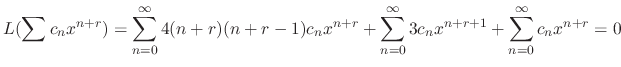
 be the least number
be the least number 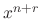 . Then
. Then
![$\displaystyle \sum_{n=0}^{\infty}[4(n+r)(n+r-1) + 1]c_{n}x^{n+r} + \sum_{n=1}^{\infty}3c_{n-1}x^{n+r} = 0. $](img1310.png)
![$\displaystyle \underbrace{(4r(r-1) + 1)c_{0}x^{r}}_{n = 0} + \sum_{n=1}^{\infty}\{[4(n+r)(n+r-1) + 1]c_{n} + 3c_{n-1}\}x^{n+r} = 0 $](img1311.png)
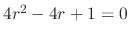 . Thus
. Thus
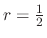 and the recurrence relation
and the recurrence relation
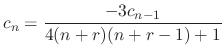
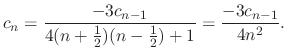
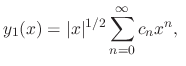 ただし
ただし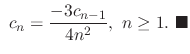
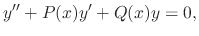
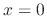 is the regular singular point and the root
is the regular singular point and the root 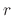 of the indicial equation is multiple root, then the linearly independent solutions
of the indicial equation is multiple root, then the linearly independent solutions 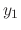 and
and 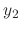 are given by the following forms.
are given by the following forms.
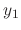 |
 |
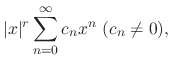 |
|
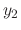 |
 |
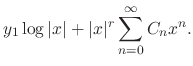 |
Now we find 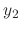 . By the theorem, we find a solution of the form
. By the theorem, we find a solution of the form
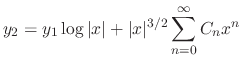
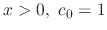 .
Substitute
.
Substitute 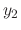 into
into 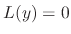 .
.
 |
 |
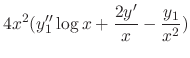 |
|
 |
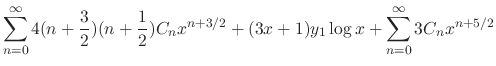 |
||
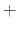 |
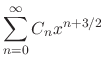 |
||
 |
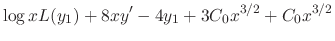 |
||
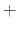 |
![$\displaystyle \sum_{n=1}^{\infty}[4(n + \frac{3}{2})(n + \frac{1}{2})C_{n} + C_{n} + 3C_{n-1}]x^{n+3/2} = 0$](img1330.png) |
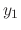 .
.
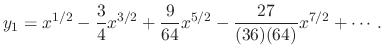
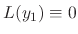 . Then
. Then
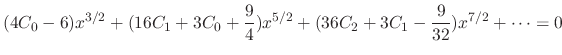
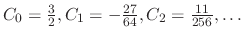 . Thus
. Thus
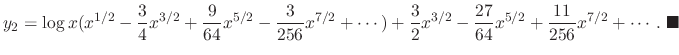
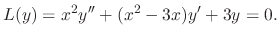
SOLUTION
Since
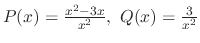 ,
, 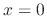 is a regular singular point. Then let
is a regular singular point. Then let
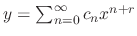 .
.
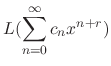 |
 |
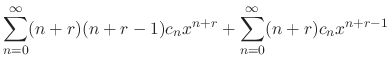 |
|
 |
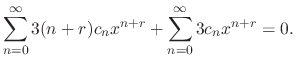 |
 be put together with
be put together with 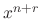 . Then
. Then
![$\displaystyle \sum_{n=0}^{\infty}[(n+r)(n+r-1) - 3(n+r) + 3]c_{n}x^{n+r} + \sum_{n=1}^{\infty}(n+r-1)c_{n-1}x^{n+r} = 0. $](img1342.png)
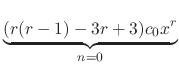 |
|||
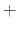 |
![$\displaystyle \sum_{n=1}^{\infty}\{[(n+r)(n+r-1) - 3(n+r) + 3]c_{n} + (n+r-1)c_{n-1}\}x^{n+r} = 0$](img1344.png) |
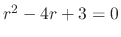 implies that
implies that 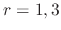 .Then we have two solutions.
.Then we have two solutions.
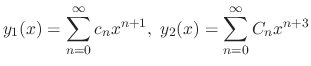
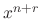 equal to 0. Then we have the following recurrence equation
equal to 0. Then we have the following recurrence equation
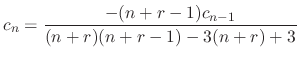
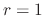 , we have
, we have
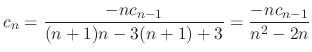
 , we have
, we have
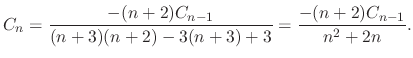
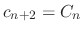 .Thus
.Thus
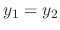 .
Then we need to find the independent solution.
.
Then we need to find the independent solution.
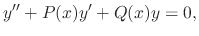
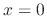 is a regular singular point and the difference of the roots
is a regular singular point and the difference of the roots
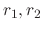 is positive integer, then the linearly independent solutions
is positive integer, then the linearly independent solutions
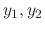 are given by the following:
are given by the following:
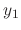 |
 |
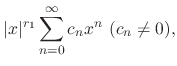 |
|
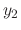 |
 |
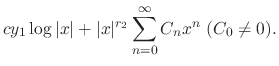 |
Thus
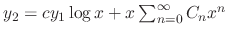 can be found by substituting
can be found by substituting 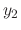 into
into
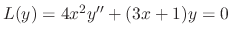 .
.
