Next: Exercise Up: Systems of differential equations Previous: Exercise Contents Index
Let 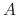 be the square matrix of order
be the square matrix of order 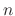 . Suppose that
. Suppose that
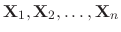 are linearly independent solutions of
are linearly independent solutions of
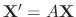 . Then
. Then
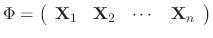
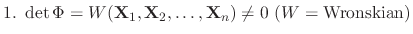
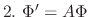
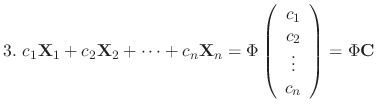
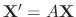 is given by
is given by
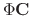 .
Now using the variation of parameter, we let
.
Now using the variation of parameter, we let
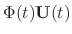 be the solution of
be the solution of
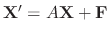 . Then since the derivative of the vector valued function is given by the derivatives of components of the vector valued function, we have
. Then since the derivative of the vector valued function is given by the derivatives of components of the vector valued function, we have
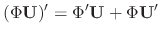
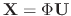 into
into
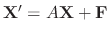 . Then
. Then
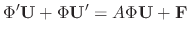
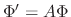 , we have
, we have
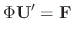
![$\displaystyle {\bf U}^{\prime} = \frac{[\Phi:{\bf F}]}{\vert\Phi\vert} $](img1117.png)
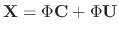
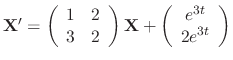
SOLUTION
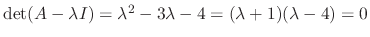 . Thus the eigenvalues are
. Thus the eigenvalues are
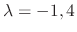 . The eigenvector corresponds to
. The eigenvector corresponds to
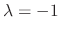 is obtained by
is obtained by
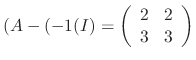 . Then the eigenvector is
. Then the eigenvector is
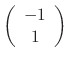 . Thus
. Thus
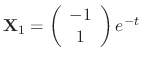 is a solution. The eigenvector corresponds to
is a solution. The eigenvector corresponds to
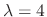 is obtained by
is obtained by
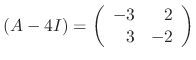 . Thus the eigenvector is
. Thus the eigenvector is
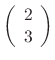 . Therefore,
. Therefore,
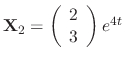 is a solution. Then the fundamental matrix is
is a solution. Then the fundamental matrix is
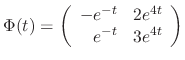
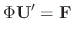
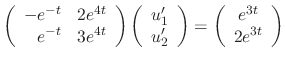
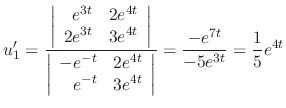
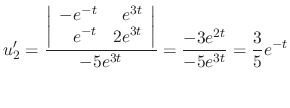
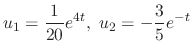
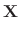 |
 |
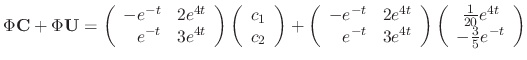 |
|
 |
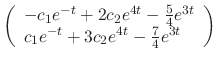 |

Let 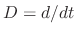 . Then
. Then
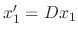 and the given differential equation
and the given differential equation
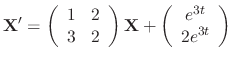
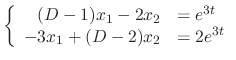
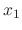 by using Cramer's rule.
by using Cramer's rule.
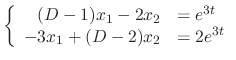 |
(3.1) |
SOLUTION Using Cramer's rule, we have
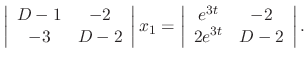
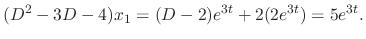
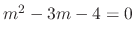 . Thus
. Thus 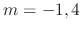 and the complementary solution
and the complementary solution 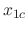 is
is
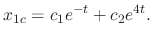
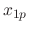 , we use the method of undetermined coefficients
, we use the method of undetermined coefficients
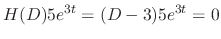
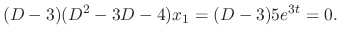
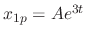 .
.
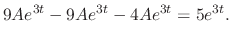
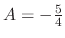 . Then
. Then
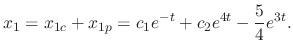
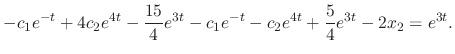
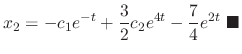
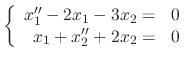
SOLUTION
Let
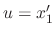 and
and
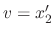 . Then
. Then
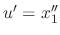 and
and
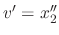 . Thus we can express
. Thus we can express
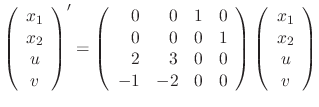
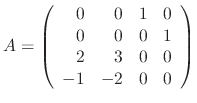 Then the eigeneqution is
Then the eigeneqution is
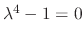 and the eigenvalues are
and the eigenvalues are
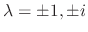 . To find the eigenvector, we use Mathematica. Then the eigenvectors correspond to
. To find the eigenvector, we use Mathematica. Then the eigenvectors correspond to
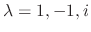 are
are
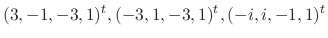
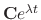 is
is
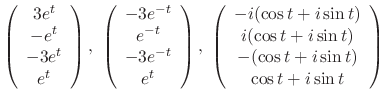
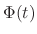 is
is
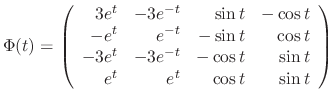
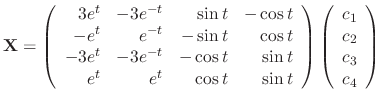
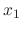 |
 |
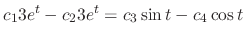 |
|
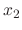 |
 |
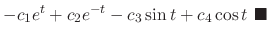 |