Next: Exercise Up: Systems of differential equations Previous: Exercise Contents Index
Let
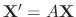 , where the matrix
, where the matrix 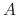 is real matrix. Suppose that
is real matrix. Suppose that
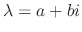 is the eigenvalue and
is the eigenvalue and
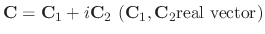 is the eigenvector for
is the eigenvector for 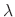 . Then by the eigenvalue equation
. Then by the eigenvalue equation
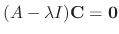
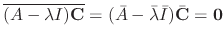
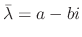 is also an eigenvalue and corresponding eigenvector is
is also an eigenvalue and corresponding eigenvector is
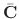 . Thus,
. Thus,
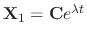 and
and
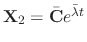 are solutions of
are solutions of
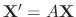 . Then the linear combination of
. Then the linear combination of
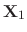 and
and
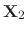 is also a solution. Therefore,
is also a solution. Therefore,
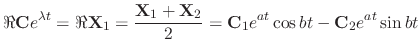
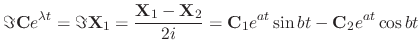
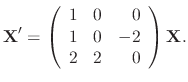
SOLUTION
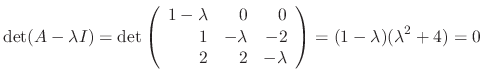
 .
.
For
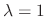 , we find the eigenvector.
, we find the eigenvector.
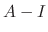 |
 |
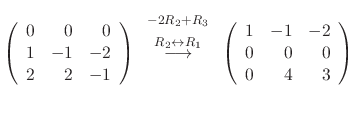 |
|
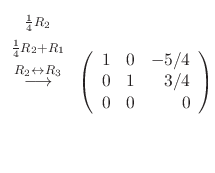 |
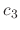 can be chosen arbitrary. Thus we let
can be chosen arbitrary. Thus we let 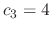 .
Then the eigenvector is
.
Then the eigenvector is
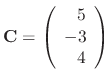 .
.
For 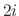 , we find the corresponding eigenvector
, we find the corresponding eigenvector
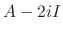 |
 |
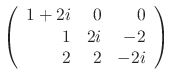 |
|
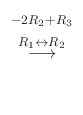 |
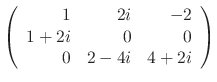 |
||
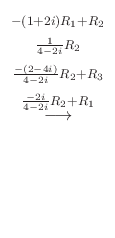 |
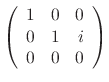 |
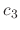 is free to choose. Thus the eigenvector is
is free to choose. Thus the eigenvector is
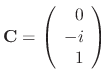 . Now we find the real part and imaginary part of
. Now we find the real part and imaginary part of
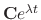 Then
Then
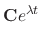 |
 |
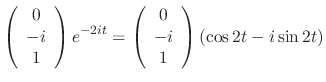 |
|
 |
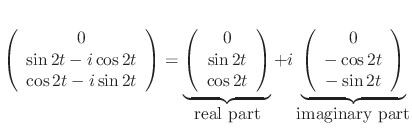 |
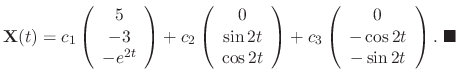
Let
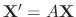 , where the matrix
, where the matrix 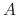 is real matrix. Suppose that
is real matrix. Suppose that 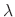 is multiple eigenvalues and
is multiple eigenvalues and 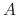 is not diagonalizable. Then cosider
is not diagonalizable. Then cosider
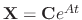 .
Since
.
Since
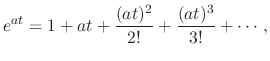
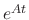 such that
such that
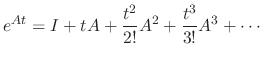
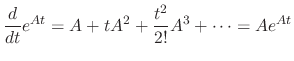
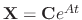 is a solution of
is a solution of
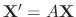 .
.
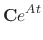 |
 |
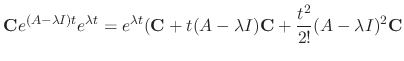 |
|
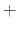 |
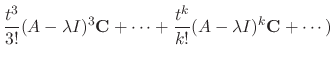 |
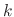 is the least number satisfing
is the least number satisfing
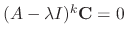 , then
, then
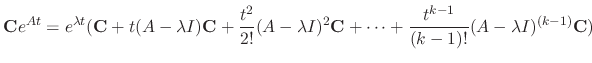
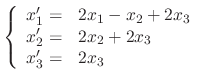
SOLUTION Since
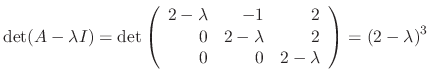
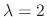 . Now we find the eigenvector C for
. Now we find the eigenvector C for
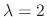 .
.
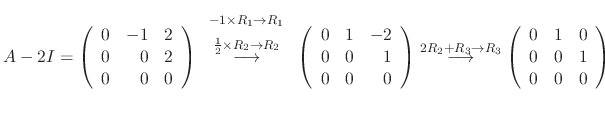
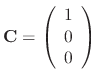 and the eigenvector is
and the eigenvector is
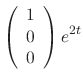
Since the degree of the matrix 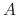 is 3, we have to find three linearly independent solutions. Thus we need to find C such that
is 3, we have to find three linearly independent solutions. Thus we need to find C such that
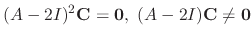
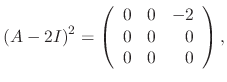
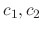 can be chosen arbitrary. Thus we let
can be chosen arbitrary. Thus we let
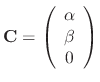 . Then
. Then
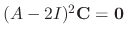 . Now we choose
. Now we choose
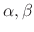 such that
such that
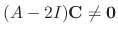 .
.
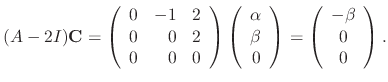
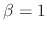 .
.
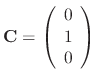 and the second solution is
and the second solution is
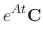 |
 |
![$\displaystyle e^{2t}e^{(A - 2I)t}{\bf C} = e^{2t}[{\bf C} + t(A - 2I){\bf C}] =...
...0&0&0
\end{array}\right)\left(\begin{array}{c}
0\\
1\\
0
\end{array}\right)\}$](img1087.png) |
|
 |
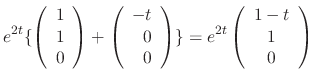 |
For the third solution, we need to find 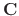 satisfying
satisfying
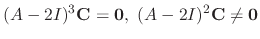
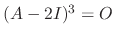 . Then
. Then
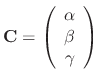 satisfies
satisfies
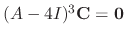 . Now
. Now
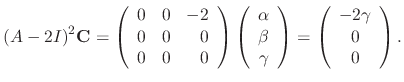
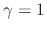 . Then
. Then
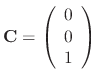 Now calculate the third solution
Now calculate the third solution
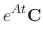 |
 |
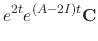 |
|
 |
![$\displaystyle e^{2t}[{\bf C} + t(A - 2I){\bf C} + \frac{t^{2}}{2!}(A - 2I)^{2}{\bf C}]$](img1098.png) |
||
 |
![$\displaystyle e^{2t}[\left(\begin{array}{c}
0\\
0\\
1
\end{array}\right) + t\...
...
0&0&0
\end{array}\right)\left(\begin{array}{c}
0\\
0\\
1
\end{array}\right)]$](img1099.png) |
||
 |
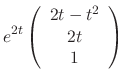 |
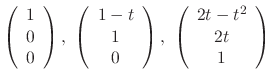 are linearly independent. Thus
are linearly independent. Thus
![$\displaystyle {\bf X} = e^{2t}[c_{1}\left(\begin{array}{c}
1\\
0\\
0
\end{arr...
...{array}{c}
2t - t^{2}\\
2t\\
1
\end{array}\right)]\ensuremath{\ \blacksquare}$](img1102.png)