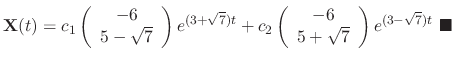Systems of linear differential equation

Consider

$\displaystyle \left\{\begin{array}{ccc} x_{1}^{\prime} &= a_{11}x_{1} + a_{12}x... ...{n1}x_{1} + a_{n2}x_{2} +& \cdots + a_{nn}x_{n} + f_{n}(t) \end{array}\right .$

Using the coefficient matrix $A$

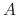and the column vector $X$

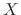anf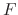

, we can express

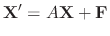
$\displaystyle {\bf X}^{\prime} = A{\bf X} + {\bf F}$

where

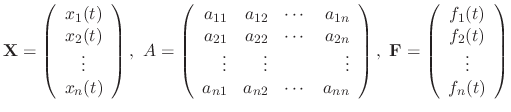
$\displaystyle {\bf X} = \left(\begin{array}{c} x_{1}(t)\\ x_{2}(t)\\ \vdots\\... ...\begin{array}{c} f_{1}(t)\\ f_{2}(t)\\ \vdots\\ f_{n}(t) \end{array}\right)$

The differentiable functions $x_{1},x_{2},\ldots,x_{n}$ satisfying the above equation is called the solution. When 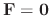${\bf F} = {\bf0}$ , we say that the differential equation is homogeneous equation.

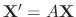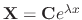We will explain how to solve ${\bf X}^{\prime} = A{\bf X}$ . Let ${\bf X} = {\bf C}e^{\lambda x}$ . Then

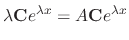
$\displaystyle \lambda {\bf C}e^{\lambda x} = A {\bf C}e^{\lambda x}$

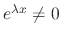Since $e^{\lambda x} \neq 0$ , we have

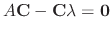
$\displaystyle A{\bf C} - {\bf C}\lambda = {\bf0}$

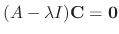
$\displaystyle (A - \lambda I){\bf C} = {\bf0}$

Here

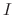denotes the unit matrix of the degree $n$

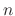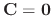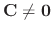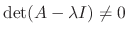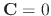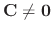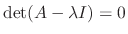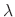. Now if ${\bf C} = {\bf0}$ , then the equation is obviously satisfied. So, we need to find the ${\bf C} \neq {\bf0}$ satisfying the above equation. Note that if ${\rm det}(A - \lambda I) \neq 0$ , then ${\bf C} = 0$ . Thus to find the ${\bf C} \neq {\bf0}$ , we have to solve $\det(A - \lambda I) = 0$ . The $\lambda$ is called the eigenvalue of the matrix $A$

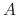and the nonzero C satisfying 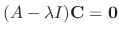$(A - \lambda I){\bf C} = {\bf0}$ is called the eigenvector for $A$

Example 3..1 Solve the following differential equation

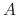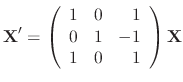
$\displaystyle {\bf X}^{\prime} = \left(\begin{array}{rrr} 1&0&1\\ 0&1&-1\\ 1&0&1 \end{array}\right){\bf X}$

SOLUTION Let 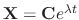${\bf X} = {\bf C}e^{\lambda t}$ . Then we have

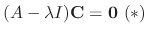
$\displaystyle (A - \lambda I){\bf C} = {\bf0}\ (*)$

Now

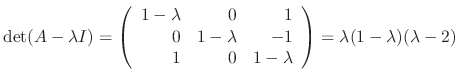
$\displaystyle \det(A - \lambda I) = \left(\begin{array}{rrr} 1-\lambda&0&1\\ 0&1-\lambda&-1\\ 1&0&1-\lambda \end{array}\right) = \lambda(1-\lambda)(\lambda -2)$

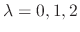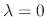Thus the eigenvalues are $\lambda = 0,1,2$ . Now we find the eigenvector for $\lambda = 0$ . Substitute 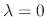$\lambda = 0$ into the equation (*). Then

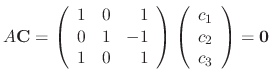
$\displaystyle A{\bf C} = \left(\begin{array}{rrr} 1&0&1\\ 0&1&-1\\ 1&0&1 \end... ...ght)\left(\begin{array}{c} c_{1}\\ c_{2}\\ c_{3} \end{array}\right) = {\bf0}$

To solve this system, we use Gaussian elimination.

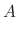$\displaystyle A$

$\displaystyle =$

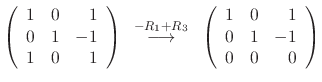$\displaystyle \left(\begin{array}{rrr} 1&0&1\\ 0&1&-1\\ 1&0&1 \end{array}\rig... ...ightarrow} \left(\begin{array}{rrr} 1&0&1\\ 0&1&-1\\ 0&0&0 \end{array}\right)$

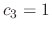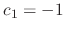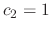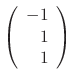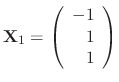Now we can let $c_{3} = 1$ . Then $c_{1} = -1$ , $c_{2} = 1$ Thus, the eigenvector C is $\left(\begin{array}{r} -1\\ 1\\ 1 \end{array}\right)$ and ${\bf X}_{1} = \left(\begin{array}{r} -1\\ 1\\ 1 \end{array}\right)$ is a solution.
For the eigenvector for $\lambda = 1$ .

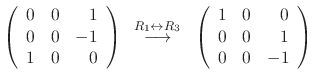$\displaystyle A - I$	$\displaystyle =$	$\displaystyle \left(\begin{array}{rrr} 0&0&1\\ 0&0&-1\\ 1&0&0 \end{array}\rig... ...ightarrow} \left(\begin{array}{rrr} 1&0&0\\ 0&0&1\\ 0&0&-1 \end{array}\right)$
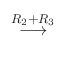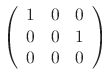	$\displaystyle \stackrel{\begin{array}{c} {}_{R_{2}+R_{3}} \end{array}}{\longrightarrow}$	$\displaystyle \left(\begin{array}{rrr} 1&0&0\\ 0&0&1\\ 0&0&0 \end{array}\right)$

Thus, we can take $c_2 = 1$

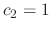. Then

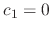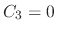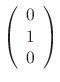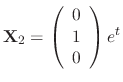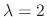
and the eigenvector is $\left(\begin{array}{r} 0\\ 1\\ 0 \end{array}\right)$ . ${\bf X}_{2} = \left(\begin{array}{r} 0\\ 1\\ 0 \end{array}\right)e^{t}$ is a solution. Similarly, we find the eigenvector corresponds to $\lambda = 2$

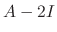$\displaystyle A - 2I$

$\displaystyle =$

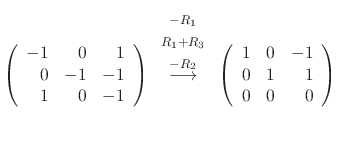$\displaystyle \left(\begin{array}{rrr} -1&0&1\\ 0&-1&-1\\ 1&0&-1 \end{array}\... ...ightarrow} \left(\begin{array}{rrr} 1&0&-1\\ 0&1&1\\ 0&0&0 \end{array}\right)$

Then we can take $c_3 = 1$

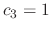and

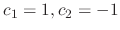. Thus the eigenvector is 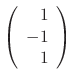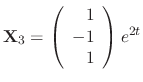$\left(\begin{array}{r} 1\\ -1\\ 1 \end{array}\right)$ . ${\bf X}_{3} = \left(\begin{array}{r} 1\\ -1\\ 1 \end{array}\right)e^{2t}$ is a solution. Since 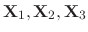${\bf X}_{1},{\bf X}_{2},{\bf X}_{3}$ are linearly independent, we have 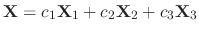${\bf X} = c_{1}{\bf X}_{1} + c_{2}{\bf X}_{2} + c_{3}{\bf X}_{3}$ and the general solution is

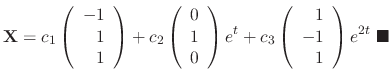
$\displaystyle {\bf X} = c_{1}\left(\begin{array}{r} -1\\ 1\\ 1 \end{array}\ri... ...egin{array}{r} 1\\ -1\\ 1 \end{array}\right)e^{2t}\ensuremath{\ \blacksquare}$

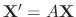Theorem 3..1 Suppose that ${\bf X}^{\prime} = A{\bf X}$ has the $n$

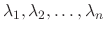different eigenvalues $\lambda_{1},\lambda_{2},\ldots,\lambda_{n}$ and corresponding eigenvectors 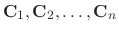${\bf C}_{1},{\bf C}_{2},\ldots,{\bf C}_{n}$ . Then the general solution is given by

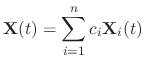
$\displaystyle {\bf X}(t) = \sum_{i=1}^{n}c_{i}{\bf X}_{i}(t)$

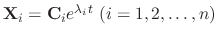where ${\bf X}_{i} = {\bf C}_{i}e^{\lambda_{i}t} \ (i = 1,2,\ldots,n)$ are the solutions of 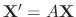${\bf X}^{\prime} = A{\bf X}$ and linearly independent.

Proof

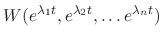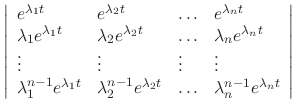$\displaystyle W(e^{\lambda_{1}t},e^{\lambda_{2}t}, \ldots e^{\lambda_{n}t})$	$\displaystyle =$	$\displaystyle \left\vert\begin{array}{llll} e^{\lambda_{1}t}& e^{\lambda_{2}t}&... ...lambda_{2}t}& \ldots & \lambda_{n}^{n-1}e^{\lambda_{n}t} \end{array}\right\vert$
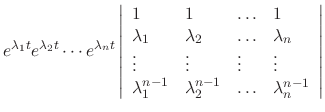	$\displaystyle =$	$\displaystyle e^{\lambda_{1}t}e^{\lambda_{2}t}\cdots e^{\lambda_{n}t}\left\vert... ...{1}^{n-1}& \lambda_{2}^{n-1}& \ldots & \lambda_{n}^{n-1} \end{array}\right\vert$
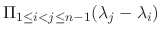	$\displaystyle =$	$\displaystyle \Pi_{1 \leq i < j \leq n-1}(\lambda_j - \lambda_i)$

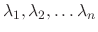Since $\lambda_{1} ,\lambda_{2} , \ldots \lambda_{n}$ are different,

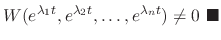
$\displaystyle W(e^{\lambda_{1}t},e^{\lambda_{2}t},\ldots, e^{\lambda_{n}t}) \neq 0\ensuremath{\ \blacksquare}$

The 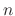$n$ linearly independent solutions of 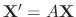${\bf X}^{\prime} = A{\bf X}$ is called the fundamental solution.

Example 3..2 Solve the following differential equation

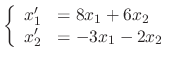$\left\{\begin{array}{rl} x_{1}^{\prime} &= 8x_{1} + 6x_{2} \\ x_{2}' &= -3x_1 - 2x_2 \end{array}\right .$ .

SOLUTION

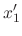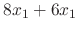$\displaystyle x_{1}^{\prime}$	$\displaystyle =$	$\displaystyle 8x_{1} + 6x_{1}$
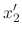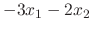$\displaystyle x_{2}^{\prime}$	$\displaystyle =$	$\displaystyle -3x_{1} - 2x_{2}$

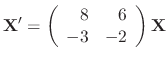
$\displaystyle {\bf X}^{\prime} = \left(\begin{array}{rr} 8&6\\ -3&-2 \end{array}\right){\bf X}$

We find the eigenvalues and eigenvectors.

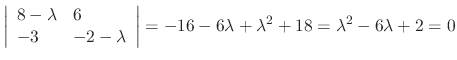
$\displaystyle \left\vert\begin{array}{ll} 8-\lambda & 6\\ -3 & -2-\lambda \end{array}\right\vert = -16-6\lambda + \lambda^2 + 18 = \lambda^2 - 6\lambda + 2 = 0$

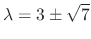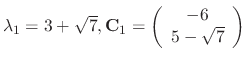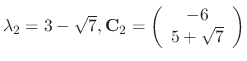Thus we have $\lambda = 3 \pm \sqrt{7}$ . For $\lambda_1 = 3 + \sqrt{7}, {\bf C}_{1} = \left(\begin{array}{c} -6\\ 5-\sqrt{7} \end{array}\right)$ . For $\lambda_{2} = 3 - \sqrt{7}, {\bf C}_{2} = \left(\begin{array}{c} -6\\ 5 + \sqrt{7} \end{array}\right)$ . Thus the general solution is

$\displaystyle {\bf X}(t) = c_{1}\left(\begin{array}{c} -6\\ 5-\sqrt{7} \end{ar... ... 5 + \sqrt{7} \end{array}\right)e^{(3-\sqrt{7})t}\ensuremath{\ \blacksquare}$

Subsections

Exercise