Next: Systems of differential equations Up: Linear Differential Equations Previous: Exercise Contents Index
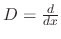 . Then we can write
. Then we can write
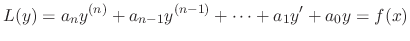
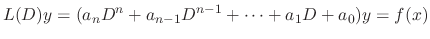
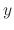 for
for
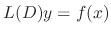 is called the Inverse operator and is expressed by
is called the Inverse operator and is expressed by
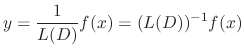
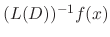 applies to the function of
applies to the function of 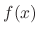 such that
such that
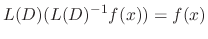
Basic rule
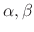 be sonstants,
be sonstants, 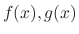 be functions. Then
be functions. Then
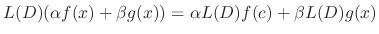
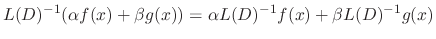
Proof The first one comes from the definition of 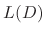 . The second one comes from the following.
. The second one comes from the following.
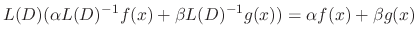
 be a constant and
be a constant and 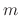 be an integer. Then
be an integer. Then
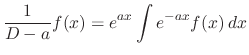
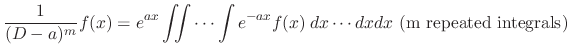
Proof Let
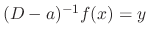 . Then
. Then
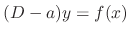 . Thus
. Thus
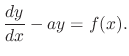
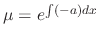 . Multiply the
. Multiply the 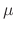 both sides
both sides
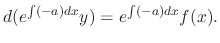
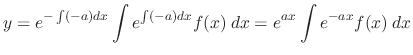
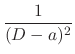 |
 |
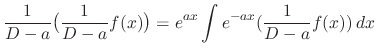 |
|
 |
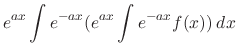 |
||
 |
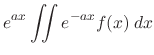 |
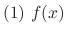 |
 |
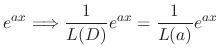 |
|
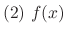 |
 |
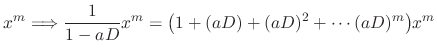 |
|
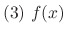 |
 |
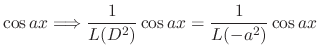 |
|
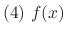 |
 |
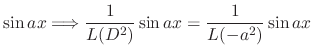 |
|
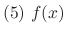 |
 |
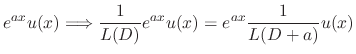 |
|
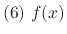 |
 |
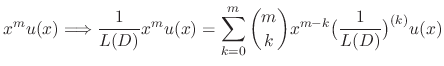 |
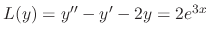 .
.
SOLUTION
The characteristic equation of 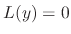 is
is
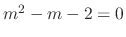 . Thus roots are
. Thus roots are 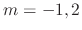 . Then the complementary solution
. Then the complementary solution 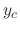 is given by
is given by
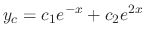
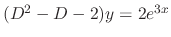 , by (1) above
, by (1) above
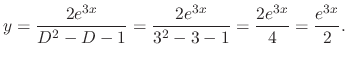
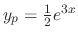 and the general solution is
and the general solution is
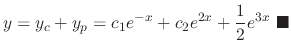
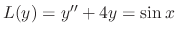 .
.
SOLUTION The characteristic equation of 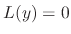 is
is
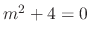 . Thus
. Thus
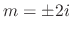 . Then the complementary solution is
. Then the complementary solution is
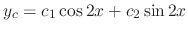
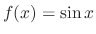 , we have
, we have
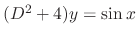 and
and
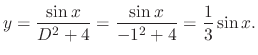
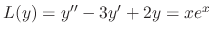
SOLUTION Let 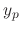 be the particular solution. Then since
be the particular solution. Then since
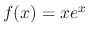 , we have
, we have
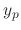 |
 |
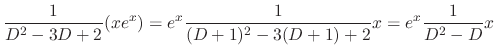 |
|
 |
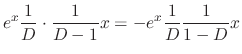 |
||
 |
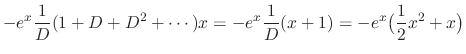 |