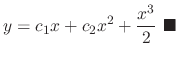Next: Exercise Up: Linear Differential Equations Previous: Exercise Contents Index
Consider 2nd-order linear differential equation with variable coefficients.
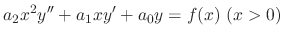
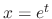 . Then for
. Then for 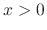 , we have
, we have
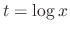 and
and
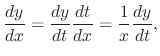
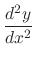 |
 |
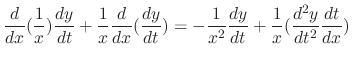 |
|
 |
 |
The characteristic equation of the Cauchy-Euler equation is given by
There is a simple way to find the indicial equation. Substitute 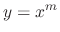 into the following differential equation.
into the following differential equation.
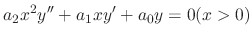
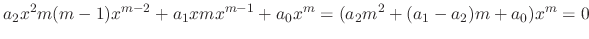
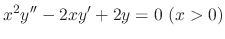
SOLUTION
Let 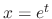 and
and 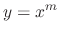 . Then the indicial equation is
. Then the indicial equation is
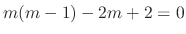 . Thus
. Thus 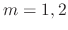 . Furtheremore, the indicial equation is the characteristic equation of
. Furtheremore, the indicial equation is the characteristic equation of
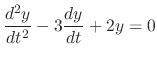
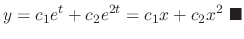
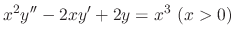
SOLUTION
The example above, we found the complementary solution is
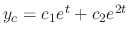 . Now since
. Now since
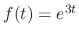 , we find the particular solution by the method of undetermined coefficients. Substitute
, we find the particular solution by the method of undetermined coefficients. Substitute
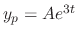 into
into
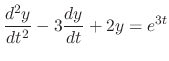
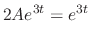
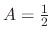 and the general solution is
and the general solution is
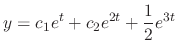
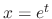 , we have
, we have