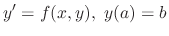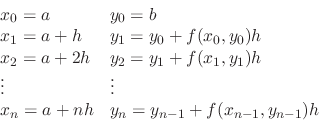Next: Exercise Up: 1st Order Differential Equation Previous: Exercise Contents Index
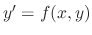 . We can think of
. We can think of 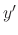 as the slope of the tangent line at
as the slope of the tangent line at 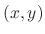 . Then consider the line starting at
. Then consider the line starting at
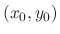 with the slope
with the slope
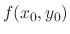 . To draw this as graph, we first draw a curve
. To draw this as graph, we first draw a curve
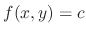 . This curve is called isocline. Now we plot points on the curve, and at each point we draw a short pointed line with the slope
. This curve is called isocline. Now we plot points on the curve, and at each point we draw a short pointed line with the slope 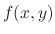 . The collection of these pointed lines are called direction field of the differential equation
. The collection of these pointed lines are called direction field of the differential equation
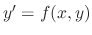 .
.
Up to this point, we try to find the general solution. Thus we ignore the singular solution. In this section, we treat the singular solution using the direction field. A general solutin with a singular solution is called the complete solution.
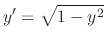 .
.SOLUTION We first find the general solution.
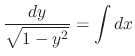
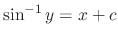
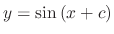
 becomes negative. But by the give differential equation,
becomes negative. But by the give differential equation,  never becomes negative. Then we draw directional fiels using isocline lines .
never becomes negative. Then we draw directional fiels using isocline lines .
From this,
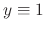 and
and
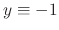 are solutions. Also,
are solutions. Also, 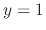 ‚Æ
‚Æ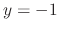 are connected with
are connected with 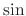 curve. Thus the complete solution is
curve. Thus the complete solution is
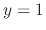 or
or 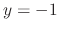 or
or
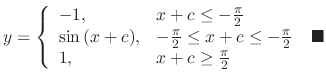
We next consider the way to obtain numerical solution from the graph.
The idea is to draw a line with the slope
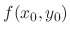 at the starting point
at the starting point 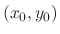 . Then the equation of line is given by
. Then the equation of line is given by
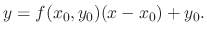
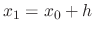 and
and
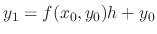 . Now with the point
. Now with the point
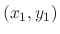 and the slope
and the slope
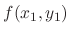 , we get
, we get
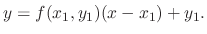
 .
.
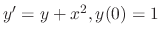 , find the value of
, find the value of 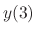 provided
provided 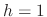 .
.
SOLUTION
Since
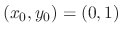 , we have
, we have 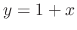 . Now since
. Now since
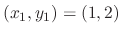 , we have
, we have
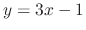 . Finally, for
. Finally, for
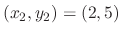 , we have
, we have
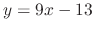 . Thus,
. Thus, 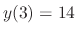 .
Note that this differential equation is linear. Thus we can find the general solution.
.
Note that this differential equation is linear. Thus we can find the general solution.
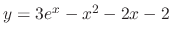 . Then
. Then
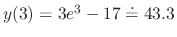

As you noticed, the error by the approximation lines is large. To make the error small, we must use smaller 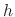 . The smaller the
. The smaller the 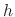 , the more calsulation for computation. Then we use computer to calculate.
, the more calsulation for computation. Then we use computer to calculate.
The more useful technique is known as Euler's method.
The approximated solution of