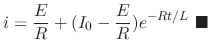Next: Exercise Up: 1st Order Differential Equation Previous: Exercise Contents Index
Given a 1st order linear differential equation in the normal form
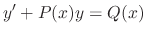
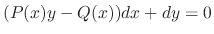
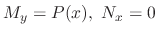
![$(1/N)[M_{y} - N_{x}] = P(x)$](img274.png) is a function of
is a function of 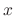 only.
Thus,
only.
Thus,
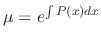
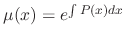 to the normal form
to the normal form
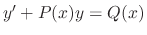 to get
to get
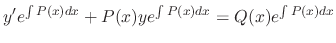
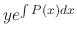 . Thus
. Thus
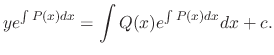
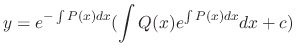
The 1st order linear differential equation can be solved by using the above formula. But it is much easier to use the integrating factor
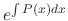 .
.
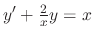 .
.SOLUTION We find the integrating factor.
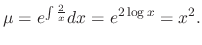
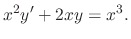
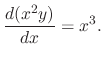
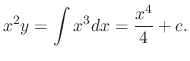
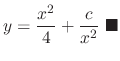
In a RLC circuit, the volatage drop by the circuit current 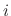 at the resistance
at the resistance 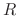 (Ħ), at the inductance
(Ħ), at the inductance 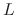 (H), and at the capacitance
(H), and at the capacitance 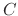 (F) is given by
(F) is given by
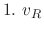 |
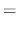 |
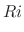 |
|
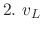 |
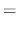 |
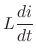 |
|
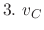 |
 |
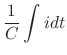 |
Then by Kirchhoff'S 2nd law,
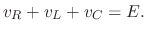
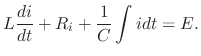
SOLUTION By Kirchhoff's voltage law,
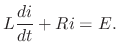
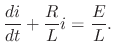
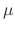 is
is 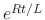 . Then multiplying
. Then multiplying 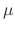 to both sides of the equation.
to both sides of the equation.
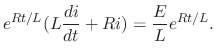
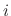 . Thus
. Thus
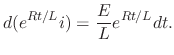
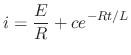
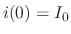 , we have
, we have
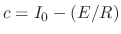 .
Therefore,
.
Therefore,