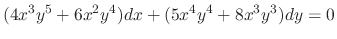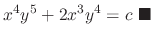Next: Exercise Up: 1st Order Differential Equation Previous: Exercise Contents Index
Suppose that
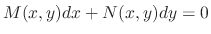 is not exact differential equation. If
is not exact differential equation. If
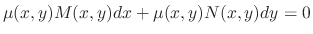
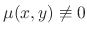 ,
then
,
then 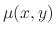 is called the integrating factor.
is called the integrating factor.
In general, an integrating factor is not unique. For example, a function 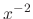 and
and 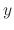 are the integrating factor of the following differential equation
are the integrating factor of the following differential equation
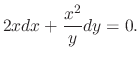
Now the question is how to find a integratin factor. Suppose that
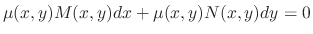
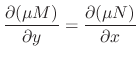
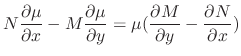
For
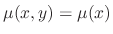 ,
,
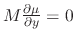 . Thus,
. Thus,
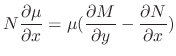
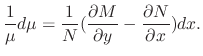
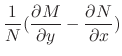
 only, then the integrating factor is given by
only, then the integrating factor is given by
![$\displaystyle \mu(x) = \exp\{\int\frac{1}{N}[M_{y} - N_{x}]dx\} $](img237.png)
For
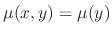 ,
,
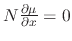 . Thus,
. Thus,
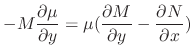
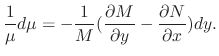
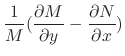
 only, then the integrating factor is given by
only, then the integrating factor is given by
![$\displaystyle \mu(y) = \exp\{-\int\frac{1}{M}[M_{y} - N_{x}]dy\} $](img243.png)
Note that since we are looking for one integrating factor, we ignore the constant.
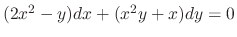 .
.
SOLUTION
Note that
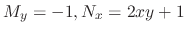 . Thus, this differential equation is not exact. Then we calculate
. Thus, this differential equation is not exact. Then we calculate
![$({1}/{N})[M_{y} - N_{x}]$](img246.png) .
.
![$\displaystyle \frac{1}{N}[M_{y} - N_{x}] = \frac{1}{x^{2}y + x}[-1 - (2xy + 1)] = -\frac{2(xy+1)}{x(xy + 1)} = -\frac{2}{x}. $](img247.png)
 only. Then the integrating factor is
only. Then the integrating factor is
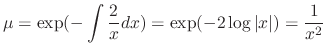
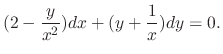
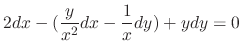
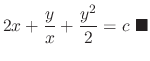
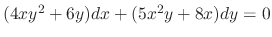 .
.
SOLUTION
Since
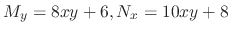 , the given differential equation is not exact. Now
, the given differential equation is not exact. Now
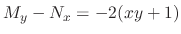 . Thus neither
. Thus neither
![$(1/N)[M_{y} - N_{x}]$](img255.png) nor
nor
![$(1/M)[M_{y} - N_{x}]$](img256.png) is a function of
is a function of  only or
only or 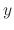 only.
Then we must find an integrating factor by the different method.
only.
Then we must find an integrating factor by the different method.
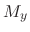 and
and 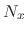 are polynomials. Then we let
are polynomials. Then we let 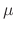 be
be
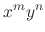 .
If
.
If
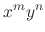 is an integrating factor, then
is an integrating factor, then
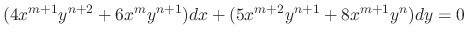
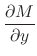 |
 |
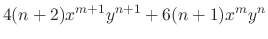 |
|
 |
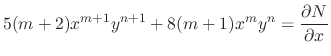 |
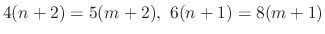
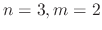 . Thus
. Thus