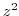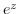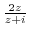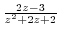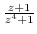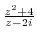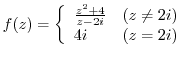Next: Analytic function,holomorphic function Up: Holomorphic function Previous: Holomorphic function Index
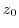 with
with
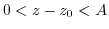 , for
, for 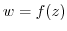 , if
, if
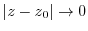 then
then
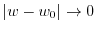 . In other words, for any positive number
. In other words, for any positive number
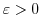 , there exists
, there exists 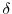 so that
so that
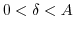 , and for any
, and for any  with
with
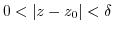 satisfies
satisfies
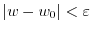 .
.  is said to have a limit
is said to have a limit 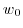 and we write
and we write
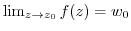 .
.
Note There are innumerable directions for
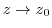 , but no matter which direction you approach
, but no matter which direction you approach 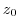 , it will be
, it will be
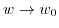 .
.
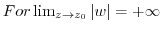 , we write
, we write
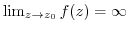 . For real-valued function, there are
. For real-valued function, there are 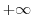 and
and 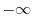 . But by the abo ve definition, for complex functions, we only have
. But by the abo ve definition, for complex functions, we only have 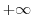 .
.
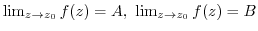 exist and the limits are finite. Then
exist and the limits are finite. Then
(1)
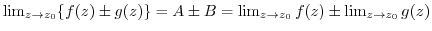
(2)
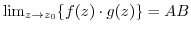
(3)
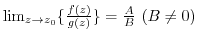
For 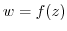 defined in the region
defined in the region  , a point
, a point 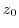 in
in  ,
,
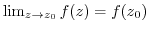 holds, In other words, for any positive number
holds, In other words, for any positive number
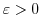 , there exists
, there exists
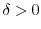 and for any
and for any  with
with
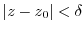 ,
,
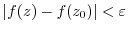 holds. Then
holds. Then  is said to be continuous at
is said to be continuous at 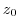 .
.
When  is continuous at each point in the region
is continuous at each point in the region  ,
,  is said to be continuous on
is said to be continuous on  .
.
(1) If
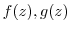 are continuous at
are continuous at 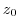 ,
,
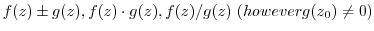 are continuous at
are continuous at 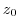 .
.
(2) Suppose that 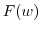 is continuous at
is continuous at 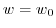 and
and 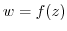 is continuous at
is continuous at 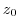 . If
. If
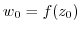 , then the composite function
, then the composite function 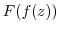 is continuous at
is continuous at 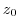 .
.
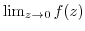 for the following
for the following  .
(1)
.
(1)
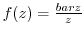
(2)
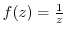
(3)
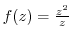
Solution
(1) Since
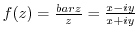 , for
, for  approaches 0 along the straight line
approaches 0 along the straight line 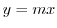 , the value of
, the value of
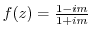 depends on the value of
depends on the value of 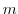 . Thus,
. Thus,
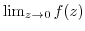 does not exist.
(2)
does not exist.
(2)
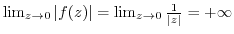 . Thus,
. Thus,
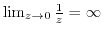
(3) For 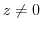 ,
,
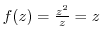 . Thus,
. Thus,
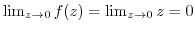 .
.
 set of points on plane excluding 0
set of points on plane excluding 0
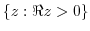
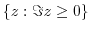
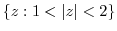
2. Find the limit of the followings.
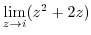
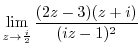
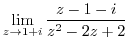
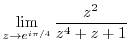
3. Find the point where the following function is not continuous.