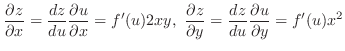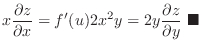Next: Higher Order Partial Derivatives Up: Partial Differentiation Previous: Tangent Plane and Normal Contents Index
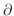 Symbol Symbol |
|---|
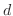 is used for the sign of derivative of a function of single variable. is used for the sign of derivative of a function of single variable. 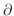 is used for the sign of derivative of a function of more than one variables. is used for the sign of derivative of a function of more than one variables.
|
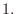 Suppose that
Suppose that
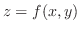 is totally differentiable and
is totally differentiable and
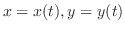 are differentiable. Then a compostite function
are differentiable. Then a compostite function
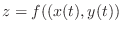 is differentiable and the following is true.
is differentiable and the following is true.
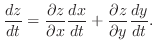
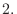 Suppose that
Suppose that
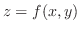 is totally differentiable and
is totally differentiable and
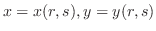 are differentiable. Then a composite function
are differentiable. Then a composite function
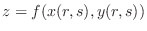 is also differentiable and the following is true.
is also differentiable and the following is true.
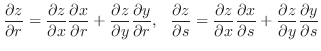
NOTE
1. Let 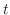 be a time,
be a time, 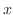 be a number of planktons,
be a number of planktons, 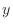 be a water temparature,
be a water temparature, 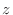 be a number of minnows. Then
be a number of minnows. Then
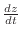 is an instanteneous change of a number of minnows with respect to a time. But a number of minnows and a number of planktons are influenced by the temparature of the water.
is an instanteneous change of a number of minnows with respect to a time. But a number of minnows and a number of planktons are influenced by the temparature of the water.
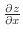 and
and
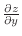 . Thus the instanteneous chage of the number of planktons with respect to the temparature is
. Thus the instanteneous chage of the number of planktons with respect to the temparature is
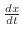 and instance change of the water temparature with respect to the time is
and instance change of the water temparature with respect to the time is
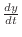 . Thus, the instanteneous change of the number of minnows with respect to the time is
. Thus, the instanteneous change of the number of minnows with respect to the time is
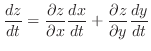
Theorem4.4 2. Express by the tree diagram. 4.22
| Tree Diagram |
|---|
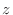 is a function of is a function of 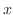 and and 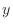 . Then draw a line from . Then draw a line from 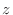 to to 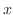 , and , and 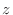 to to 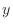 . Now . Now 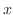 and and 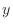 are functions of are functions of 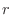 and and 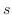 . Then draw lines from . Then draw lines from 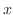 and and 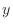 to to 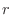 and and 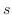 . .
|
Proof
2.
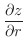 |
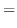 |
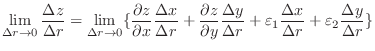 |
|
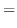 |
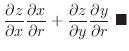 |
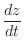
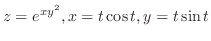 2.
2.
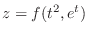
SOLUTION 1.
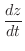 |
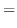 |
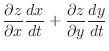 |
|
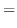 |
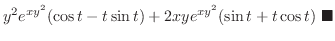 |
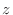 is a function of
is a function of 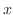 and
and 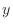 ,
, 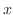 and
and 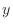 are functions of
are functions of 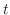 . Then draw a line from
. Then draw a line from 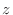 to
to 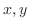 and lines from
and lines from 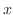 to
to 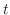 , from
, from 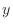 to
to 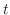 .
.
2. Let
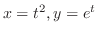 . Then
. Then
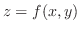 and
and
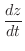 |
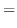 |
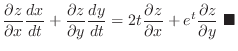 |
Since
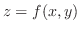 is not known,
is not known,
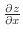 is the final form
is the final form
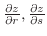 of the following function.
of the following function.
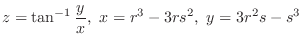
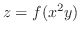 , Show
, Show
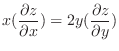 .
.
SOLUTION 1.
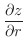 |
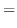 |
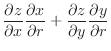 |
|
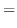 |
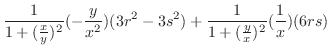 |
||
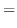 |
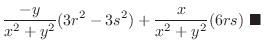 |
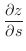 |
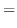 |
 |
|
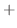 |
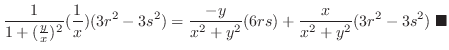 |
2. Let
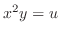 . Then
. Then 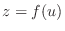 and by the tree diagram,
and by the tree diagram,