next up previous contents index
Next: 1.2 Trigonometric Functions Up: ANSWERS Previous: 0.2 INEQUALITIES   Contents   Index

1.1 Functions

1.

(a) $f(1) = 1$ (b) $f(1) = 13$ (c) $f(1) = 2$

2.

(a) Domain(f) $= (-\infty, \infty)$ Range(f) $= [-1, \infty)$．

(b) Domain(f) $= [1, \infty)$ Range(f) $= [0, \infty)$．

(c) Domain(f) $= (-\infty, \infty)$ Range(f) $= [0, 1]$．

3.

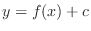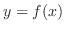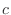(a) The graph of $y = f(x) + c$ is a parallel shift of the graph of $y = f(x)$ by $c$ into the positive 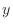$y$-axis direction．

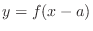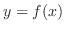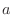(b) The graph of $y = f(x - a)$ is a parallel shift of the graph of $y = f(x)$ by $a$ into the positive 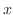$x$-axis direction．

\begin{figure}\begin{center}\includegraphics[width=5cm]{CALCFIG/ren1-1-3a.eps}\e... ...enter}\includegraphics[width=5cm]{CALCFIG/ren1-1-3b.eps}\end{center}\end{figure}

4.

(a) $\displaystyle{(f \circ g)(x) = 2x^{2} + 5}$ $\displaystyle{g(f(x)) = (2x+5)^{2}}$ (b) $(f \circ g)(x) = x$ $g(f(x)) = x$

(c) $\displaystyle{(f \circ g)(x) = \frac{x^{4}}{1 + x^{2}}}$ $\displaystyle{g(f(x)) = x^{2}(x+1)^{2}}$

5.

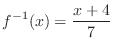(a) $\displaystyle{f^{-1}(x) = \frac{x+4}{7}}$ (b) $\displaystyle{y = \sqrt[3]{x-2} - 1}$ (c) is not one-to-one．

6.

(a) odd function (b) odd function