Next: Repeated Integrals Up: Multiple Integrals Previous: Multiple Integrals Contents Index
Let
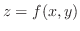 be a bounded function on the rectangular region
be a bounded function on the rectangular region 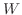 over the
over the 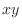 -plane. Divide the rectangular region
-plane. Divide the rectangular region 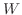 by the straight lines parallel to
by the straight lines parallel to  -axis and
-axis and  -axis and denote the partitioned small rectangles by
-axis and denote the partitioned small rectangles by
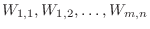 . We denote this partition by
. We denote this partition by 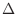 .
Now for each
.
Now for each 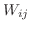 , take an arbitrary point
, take an arbitrary point 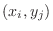 and consider the sum of small rectangular parallelpiped
and consider the sum of small rectangular parallelpiped  . Let
. Let
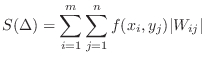
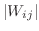 is the area of
is the area of 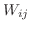 and
and 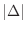 is the longest diagonal of
is the longest diagonal of 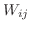 .
If
.
If  approaches the same value as
approaches the same value as 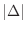 approaches 0 independent of the partition and the choice of
approaches 0 independent of the partition and the choice of 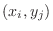 , then
, then  is called Double Integrable on
is called Double Integrable on 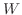 .
.
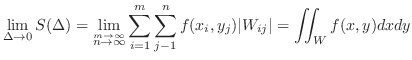
| Sum |
|---|
 is written as is written as
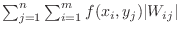 . Thus add the small rectangular parallelpiped in the direction of . Thus add the small rectangular parallelpiped in the direction of  -axis, then add in the direction of -axis, then add in the direction of  -axis is the same as add the small rectangular parallelpiped in the direction of -axis is the same as add the small rectangular parallelpiped in the direction of  -axis, then add in the direction of -axis, then add in the direction of  -axis. This is the basic concept of the repeated integrals. -axis. This is the basic concept of the repeated integrals.
|
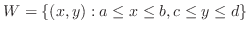 . If
. If  is continuous on
is continuous on 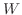 , then
, then
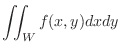 |
 |
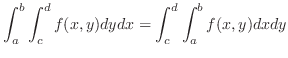 |
NOTE Fix  and conside the integration of
and conside the integration of  from
from 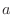 to
to 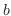 with respect to
with respect to  . Then we have
. Then we have
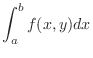
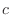 to
to 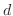 with respect to
with respect to  to obtain
to obtain
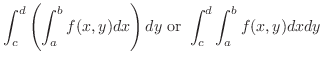
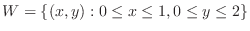 . Evaluate the following repeated integral
. Evaluate the following repeated integral
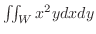 .
.
SOLUTION
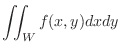 |
 |
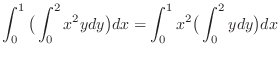 |
|
 |
![$\displaystyle \int_0^1 x^2 \big(\big[\frac{y^2}{2}\big]_{0}^{2}\big)dx$](img1019.png) |
||
 |
![$\displaystyle \int_0^1 2x^2 dx = \big[\frac{2}{3}x^3\big]_0^1 = \frac{2}{3}$](img1020.png) |
We evaluate
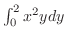 by keeping
by keeping  as a constant.
as a constant.
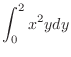 |
 |
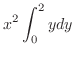 |
|
 |
![$\displaystyle x^2 [\frac{y^2}{2}]_0^2$](img1024.png) |
||
 |
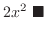 |
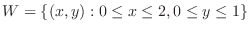 . Evaluate the following repeated integrals
. Evaluate the following repeated integrals
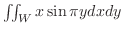 .
.
| Exercise5-1 |
|---|
It is possible to evaluate
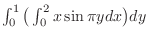 . .
|
SOLUTION
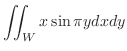 |
 |
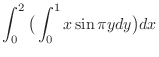 |
|
 |
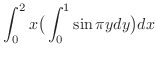 |
||
 |
![$\displaystyle \int_0^2 x \big(\big[-\frac{1}{\pi}\cos{\pi y}\big]_0^1\big)dx$](img1032.png) |
||
 |
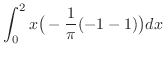 |
||
 |
![$\displaystyle \int_0^2 \frac{2}{\pi}x dx = \big[\frac{2}{\pi}(\frac{x^2}{2})\big]_0^2 = \frac{2}{\pi}(\frac{4}{2}) = \frac{4}{\pi} \ensuremath{ \blacksquare}$](img1034.png) |
Let
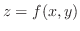 be a function defined on the closed bounded region
be a function defined on the closed bounded region  on
on 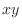 -plane. Let
-plane. Let 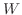 be a rectangular region containing
be a rectangular region containing  . Now divide the rectangular region
. Now divide the rectangular region 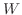 by the straight lines parallel to
by the straight lines parallel to  -axis and
-axis and  -axis and denote the partitioned small rectangles by
-axis and denote the partitioned small rectangles by
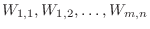 .
.
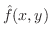 be the function on
be the function on  defined by
defined by
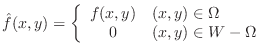
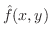 is integrable on
is integrable on  , then we say
, then we say  is integrable on
is integrable on  and the integration of
and the integration of  on
on  is expressed as follows:
is expressed as follows:
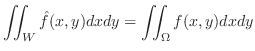
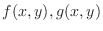 are continuous on
are continuous on  . Then we have the followings.
. Then we have the followings.
1. Let 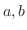 be constants. Then
be constants. Then
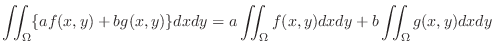
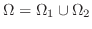 , then
, then
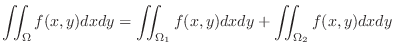
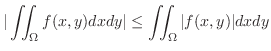
| Understanding |
|---|
If the region  is not a rectangular region, then consider the rectangle containing is not a rectangular region, then consider the rectangle containing  . For the rectangle inside of . For the rectangle inside of  , use , use  as it is given. For the rectangular region outside of as it is given. For the rectangular region outside of  , we set , we set
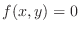 . This way we can define repeated integral over . This way we can define repeated integral over  . .
|
| Linearity |
|---|
| Theorem5-2-1. is called linearity of double integral. |