Next: Integration by Substitution Up: Integration Previous: Integration Contents Index
 defined on some interval
defined on some interval 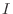 . Then a function
. Then a function 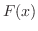 safisfies
safisfies
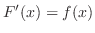
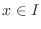 is called primitive function of
is called primitive function of  .
.
| Understanding |
|---|
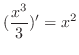 . Then a function . Then a function
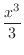 is a primitive function of is a primitive function of
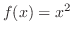 . Similarly, since . Similarly, since
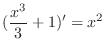 , ,
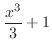 is a primitive function of is a primitive function of
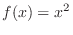 . .
|
Antiderivatives
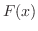 be a primitive function of
be a primitive function of  . Then every primitive function of
. Then every primitive function of  is given by
is given by 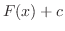 , where
, where 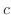 is an arbitrary constant.
is an arbitrary constant.
Proof
Let 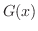 be a primitive function of
be a primitive function of  . Then
. Then
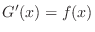 and since
and since
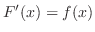 ,
,
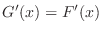 . Now let
. Now let
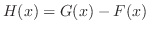 . Then
. Then 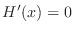 . This means that
. This means that
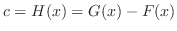 , where
, where 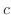 is constant. Thus
is constant. Thus
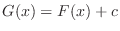 .
Note that
.
Note that
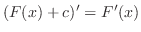

| Understanding |
|---|
Let 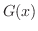 and and 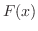 be primitive functions of be primitive functions of  . Then . Then
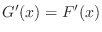 . This means that the slope of the tangent line to . This means that the slope of the tangent line to 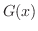 and the slope of the tangent line to and the slope of the tangent line to 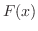 is the same for all is the same for all  . Thus the graph of . Thus the graph of 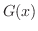 and and 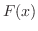 are parallet. Thus, the difference of are parallet. Thus, the difference of 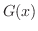 and and 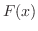 is constant. is constant.
|
Antiderivatives
Every primitive function of  is called a antiderivative and denoted by
is called a antiderivative and denoted by
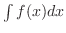 .
.
Antiderivative Suppoe 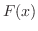 is a primitive function of
is a primitive function of  . Then
. Then
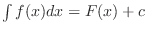 .
We call this
.
We call this  integrand.
integrand.
The process of finding an antiderivative of  is calle antidifferentiation or integration.
is calle antidifferentiation or integration.
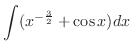
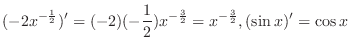 .
Then since the derivative of a sum is the sum of the derivatives,
.
Then since the derivative of a sum is the sum of the derivatives,
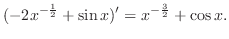
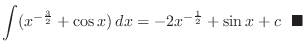
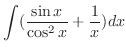
SOLUTION Note that
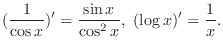
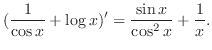
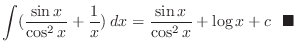
| Check |
|---|
Find 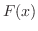 satisfying satisfying
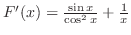 . .
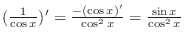 . .
|
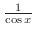 as
as 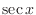 . Express
. Express
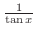 as
as 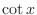 .
Integration Formulas
.
Integration Formulas
| Theorem3.2-10. |
|---|
The derivative of
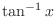 is already derived in Exercise2.7 and is is already derived in Exercise2.7 and is
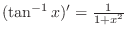 . .
|
NOTE Differentiate the right-hand side to get the integrand.
1.
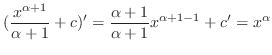 . Thus,
. Thus,
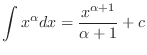
10.
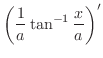 |
 |
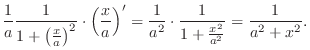 |
Rules of Integration
NOTE
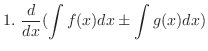 |
 |
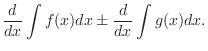 |
|
 |
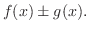 |
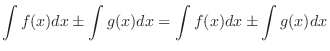
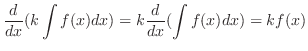
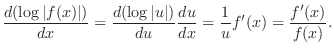
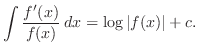
| Rules of Integration |
|---|
| 1. The integral of a sum is the sum of the integrals.
2. The integral of a constant multiple is the constant multiple of the integral. 3. The integral of a function whose numerator is the derivative of the denominator is a log of the absolute value of the denominator. |
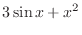 2.
2.
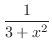 3.
3.
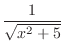
In this problem, the rules of the integral of a sum and the interal of a constant multiple can be used.
SOLUTION
1.
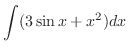 |
 |
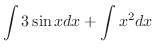 |
|
 |
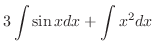 |
||
 |
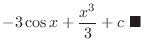 |
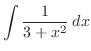 |
 |
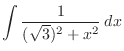 |
|
 |
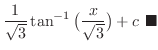 |
Use
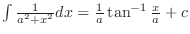 .
.
3.
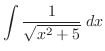 |
 |
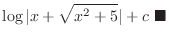 |
Use
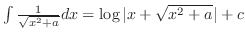 .
.
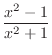 2.
2.
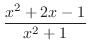 3.
3.
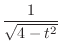 4.
4.
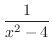
SOLUTION
 .
1.
.
1.
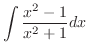 |
 |
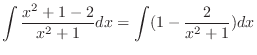 |
|
 |
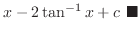 |
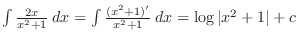 . Now since
. Now since
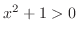 , we write
, we write
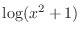 .
.
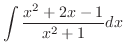 |
 |
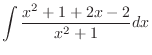 |
|
 |
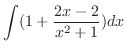 |
||
 |
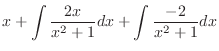 |
||
 |
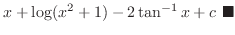 |
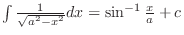 .
.
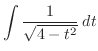 |
 |
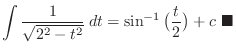 |
Write
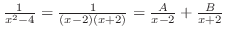 . Then find
. Then find 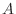 and
and 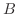 .
4.
.
4.
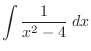 |
 |
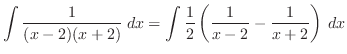 |
|
 |
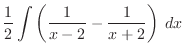 |
||
 |
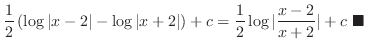 |
Alternative solution By the rule of the integration, we have
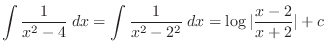
|
Exercise A
|
|
Exercise B
|