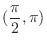Next: Exponential Functions/Logarithmic Functions Up: Continous functions Previous: Continous functions Contents Index
 be a continuous function on
be a continuous function on ![$[a,b]$](img1050.png) . Suppose that
. Suppose that 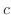 is a real number satisfying
is a real number satisfying
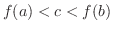 . Then there exists
. Then there exists
![$\xi \in [a,b]$](img1052.png) so that
so that
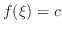 .
.
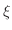 is called ksi or gzai
is called ksi or gzai
NOTE Intermediate Value Theorem tells that any continuously varying function takes all values in between. Extreme Value Theorem
 is continuous on
is continuous on ![$[a,b]$](img1050.png) . Then there exists at least one number
. Then there exists at least one number 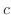 and
and 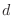 which attains a maximum and minimum.
which attains a maximum and minimum.
NOTE  attains a maximum in
attains a maximum in ![$[a,b]$](img1050.png) iff the following two conditions are satisfied.
iff the following two conditions are satisfied.
![$x \in [a,b]$](img1057.png) , there exists
, there exists 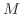 so that
so that
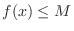 .
.
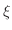 in
in ![$[a,b]$](img1050.png) such that
such that
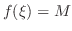 .
.
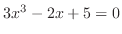 has at least one real valued solution.
has at least one real valued solution.
SOLUTION
Note that a equation has a real-valued solution if and only if the graph of the function representing a equation has an intersection with  -axis.
Let
-axis.
Let
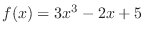 . Find
. Find  so that the value of
so that the value of  is positive and the value of
is positive and the value of  is negative. For example,
is negative. For example,
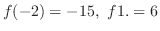
What is important here is the existence of a slution. So, we do not have to solve the equation.
Short cut Before evaluating 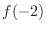 , we write
, we write
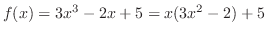 . Then,
. Then,
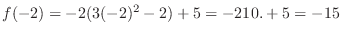
Since  is continuous on
is continuous on ![$[-2,1]$](img1067.png) , no matter how you draw a curve between the points
, no matter how you draw a curve between the points 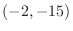 and
and 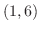 , the curve has a point in common. let this point be
, the curve has a point in common. let this point be 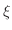 . Then
. Then
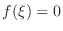 and this
and this 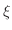 is a real-valued solution of
is a real-valued solution of
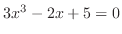

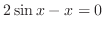 has a real-valued solution in
has a real-valued solution in
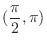 .
. If a function changes sign at some point, then the value at the point is 0.
SOLUTION Let
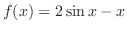 . Then
. Then
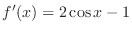 and
and
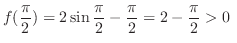 or
or 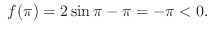
 is continuous on
is continuous on
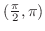 , by the Intermediate Value Theorem, there exists
, by the Intermediate Value Theorem, there exists
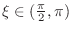 such that
such that
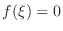

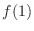 so that the following functions become continuous at
so that the following functions become continuous at 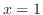
![[*]](crossref.png) renshu:1-4-4
renshu:1-4-4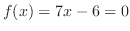 on the interval
on the interval ![$[0,1]$](img1094.png) within the error less than 0.1
within the error less than 0.1
![[*]](crossref.png) enshu:1-4-2
enshu:1-4-2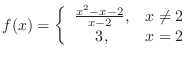 is continous at
is continous at 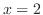 .
.
![[*]](crossref.png) enshu:1-4-3
enshu:1-4-3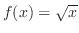 is continuous on the interval
is continuous on the interval
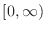
![[*]](crossref.png) enshu:1-4-5
enshu:1-4-5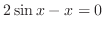 has a real solution in the interval
has a real solution in the interval