Next: Triple Integrala Up: Application of Double Integrals Previous: Surface Area Contents Index
Given a closed bounded region  and continuous functions
and continuous functions
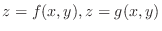 on
on  , and suppose that
, and suppose that
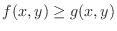 on
on  . Then the volume of solid bounded by the lines parallel to
. Then the volume of solid bounded by the lines parallel to 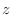 -axis through the boundary
-axis through the boundary
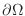 and the surfaces
and the surfaces 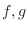 is given by
is given by
![$\displaystyle V = \iint_{\Omega}[f(x,y) - g(x,y)]dxdy $](img1486.png)
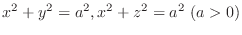 .
.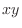 -plane is
-plane is
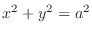 and
and 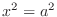 . Thus,
. Thus,
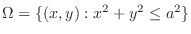 . Also
. Also
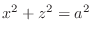 implies
implies
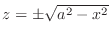 . Thus the upper surface is
. Thus the upper surface is
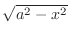 and the lower surface is
and the lower surface is
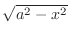 over
over  . From this, the volume of the solid is set up by
. From this, the volume of the solid is set up by
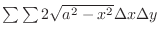 , where
, where
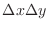 represents the small rectangle of base area and
represents the small rectangle of base area and
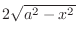 represents the height of a small solid cylinder.
Now use vertically simple region for
represents the height of a small solid cylinder.
Now use vertically simple region for  . Then
. Then
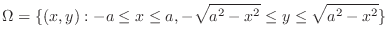
 |
 |
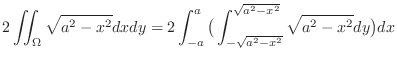 |
|
 |
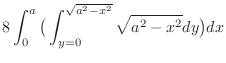 |
||
 |
![$\displaystyle 8\int_{0}^{a}\big[\sqrt{a^2 - x^2}y\big]_0^{\sqrt{a^2 - x^2}}dx$](img1500.png) |
||
 |
![$\displaystyle 8\int_{0}^{a}(a^2 - x^2)dx = 8\left[a^2 x - \frac{x^3}{3}\right ]_{0}^{a} = \frac{16a^3}{3}
\ensuremath{ \blacksquare}$](img1501.png) |
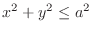 and
and
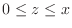 .
.
SOLUTION Note that the solid is bounded by the surface goes through the boundary of
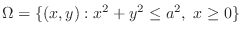 and parallel to the
and parallel to the 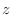 -axis, and the plane
-axis, and the plane 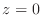 ,
, 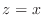 .
Using the polar coordinate to express
.
Using the polar coordinate to express  . Since
. Since
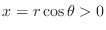 ,
,
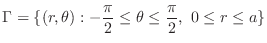
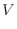 |
 |
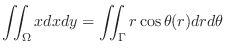 |
|
 |
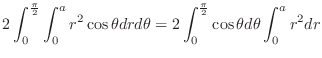 |
||
 |
![$\displaystyle 2\left[\sin{\theta}\right]_{0}^{\frac{\pi}{2}}\left[\frac{r^3}{3}\right]_{0}^{a} = \frac{2a^3}{3}\ensuremath{ \blacksquare}$](img1515.png) |
(a) The region enclosed by
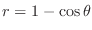
(b) Inside of the curve
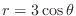 and outside of the curve
and outside of the curve
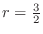 .
.
(c) Inside of the curve
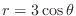 and outside of the curve
and outside of the curve
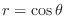
(a)
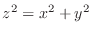 with
with
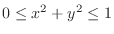 ,
, 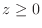 .
.
(b) 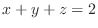 with
with
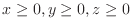 .
.
(c) 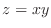 with
with
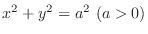 .
.
(a)
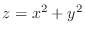 with
with 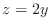
(b)
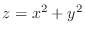 with
with
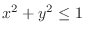
(a) Sphere
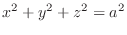 with the radius
with the radius 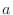 .
.
(b) 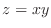 with
with
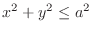
(c)
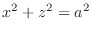 and
and
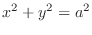 .
.
(d) The surface generated by rotating
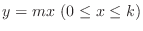 about
about 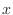 -axis for
-axis for 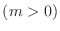 .
.
(a)
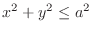 with
with
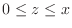
(b)
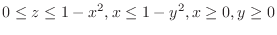 .
.
(c)
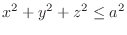 and
and
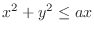 .
.
(d)
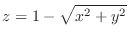 and
and 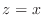 ,
, 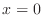 .
.