Area

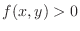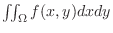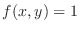For $f(x,y) > 0$ , the double integral $\iint_{\Omega}f(x,y)dxdy$ represents the volume of a solid whose base area is $\Omega$ and the height is $f(x,y)$ . If $f(x,y) = 1$ , then the double integral 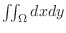$\iint_{\Omega}dxdy$ can be thought of the volume of solid whose base area is $\Omega$ and the height is 1. Now ignore the unit, then we can think of the area of $\Omega$ . Thus

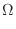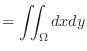
$\displaystyle \Omega$ base area $\displaystyle = \iint_{\Omega}dxdy$

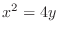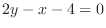
Example 5..6 Find the area of the region $\Omega$ bounded by the curve $\displaystyle{x^2 = 4y}$ and the line $\displaystyle{2y - x - 4 = 0}$

SOLUTION First find the intersection of two curves. Let 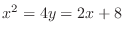$x^2 = 4y = 2x + 8$ . Then 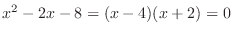$x^2 - 2x - 8 = (x-4)(x+2) = 0$ which implies $x = -2,4$ .

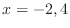$% latex2html id marker 30413 \includegraphics[width=4.5cm]{SOFTFIG-5/reidai5-6.eps}$

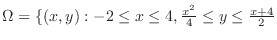Now using the vertical simple, we have $\Omega = \{(x,y): -2 \leq x \leq 4, \frac{x^2}{4} \leq y \leq \frac{x+4}{2}$ . Then

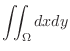$\displaystyle \iint_{\Omega}dxdy$	$\displaystyle =$	$\displaystyle \int_{-2}^{4}dx\int_{\frac{x^2}{4}}^{\frac{x+4}{2}}dy = \int_{-2}^{4}[\frac{x+4}{2} - \frac{x^2}{4}]dx$
	$\displaystyle =$	$\displaystyle \left[\frac{x^2}{4} +2x - \frac{x^3}{12}\right ]_{-2}^{4} = \frac{16 - 4}{4} + 2(4+2) -\frac{1}{12}(64 + 8)$
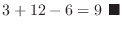	$\displaystyle =$	$\displaystyle 3 + 12 - 6 = 9 \ensuremath{ \blacksquare}$

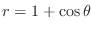Exercise 5..6 Find the area of the region $\Omega$ that lies inside the cardioid $\displaystyle{r = 1 + \cos{\theta}}$ but outside the circle $r = 1$

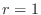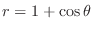SOLUTION First find the intersection of $r = 1 + \cos{\theta}$ and $r = 1$

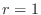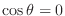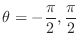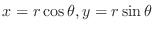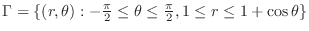. Then since $\cos{\theta} = 0$ , $\displaystyle{\theta = -\frac{\pi}{2}, \frac{\pi}{2}}$ . Thus by change of variables, $x = r\cos{\theta}, y = r\sin{\theta}$ , the region $\Omega$ is transformed into the region $\Gamma = \{(r,\theta) : -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}, 1 \leq r \leq 1+\cos{\theta} \}$ . Thus

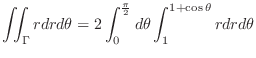$\displaystyle \iint_{\Omega}dxdy$	$\displaystyle =$	$\displaystyle \iint_{\Gamma}rdrd\theta = 2\int_{0}^{\frac{\pi}{2}}d\theta \int_{1}^{1+\cos{\theta}}rdrd\theta$
	$\displaystyle =$	$\displaystyle 2\int_{0}^{\frac{\pi}{2}} \left[\frac{r^2}{2}\right ]_{1}^{1+\cos... ...ta = 2\int_{0}^{\frac{\pi}{2}}\frac{2\cos{\theta} + \cos^{2}{\theta}}{2}d\theta$
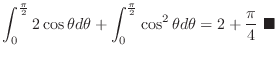	$\displaystyle =$	$\displaystyle \int_{0}^{\frac{\pi}{2}} 2\cos{\theta}d{\theta} + \int_{0}^{\frac... ...}{2}} \cos^{2}{\theta}d{\theta} = 2 + \frac{\pi}{4} \ensuremath{ \blacksquare}$